决策树
数据分析最难的部分在数据挖掘,数据挖掘需要用到大量的分析算法
我们先来学习下决策树相关的算法,下图为一个打篮球的训练集
如果我们要出门打篮球,一般会根据“天气”、“温度”、“湿度”、“刮风”这几个条件来判断,最后得到结果:去打篮球或者不去
我们在做决策树的时候,会经历两个阶段:构造和剪枝
构造
什么是构造呢?构造就是生成一棵完整的决策树
简单来说,构造的过程就是选择什么属性作为节点的过程,那么在构造过程中,会存在三种节点
- 根节点:就是树的最顶端,最开始的那个节点。在上图中,“天气”就是一个根节点
- 内部节点:就是树中间的那些节点,比如说“温度”、“湿度”、“刮风”
- 叶节点:就是树最底部的节点,也就是决策结果
节点之间存在父子关系。比如根节点会有子节点,子节点会有子子节点,但是到了叶节点就停止了,叶节点不存在子节点
在构造过程中,需要解决三个重要的问题
- 选择哪个属性作为根节点
- 选择哪些属性作为子节点
- 什么时候停止并得到目标状态,即叶节点
剪枝
剪枝就是给决策树瘦身,这一步想实现的目标就是,不需要太多的判断,同样可以得到不错的结果
之所以这么做,是为了防止“过拟合”(Overfitting)现象的发生
“过拟合”是指模型的训练结果“太好了”,以至于在实际应用的过程中,会存在“死板”的情况,导致分类错误
造成过拟合的原因之一就是因为训练集中样本量较小。如果决策树选择的属性过多,构造出来的决策树一定能够“完美”地把训练集中的样本分类
但是这样就会把训练集中一些数据的特点当成所有数据的特点,但这个特点不一定是全部数据的特点,这就使得这个决策树在真实的数据分类中出现错误,也就是模型的“泛化能力”差
泛化能力指的分类器是通过训练集抽象出来的分类能力,你也可以理解是举一反三的能力
如果我们太依赖于训练集的数据,那么得到的决策树容错率就会比较低,泛化能力差
因为训练集只是全部数据的抽样,并不能体现全部数据的特点。所以我们可以对决策树进行剪枝
一般来说,剪枝可以分为“预剪枝”(Pre-Pruning)和“后剪枝”(Post-Pruning)
- 预剪枝是在决策树构造时就进行剪枝。方法是在构造的过程中对节点进行评估
- 如果对某个节点进行划分,在验证集中不能带来准确性的提升,那么对这个节点进行划分就没有意义,这时就会把当前节点作为叶节点,不对其进行划分
- 后剪枝就是在生成决策树之后再进行剪枝,通常会从决策树的叶节点开始,逐层向上对每个节点进行评估
- 如果剪掉这个节点子树,与保留该节点子树在分类准确性上差别不大,或者剪掉该节点子树,能在验证集中带来准确性的提升,那么就可以把该节点子树进行剪枝
- 方法是:用这个节点子树的叶子节点来替代该节点,类标记为这个节点子树中最频繁的那个类
简单一句话总结,就是过拟合(以偏概全),欠拟合(提取特征不足)
如何判断要不要去打篮球
训练集数据
| 天气 | 温度 | 湿度 | 刮风 | 是否打篮球 |
|---|---|---|---|---|
| 晴天 | 高 | 中 | 否 | 否 |
| 晴天 | 高 | 中 | 是 | 否 |
| 阴天 | 高 | 高 | 否 | 是 |
| 小雨 | 高 | 高 | 否 | 是 |
| 小雨 | 低 | 高 | 否 | 否 |
| 晴天 | 中 | 中 | 是 | 是 |
| 阴天 | 中 | 高 | 是 | 否 |
天气、温度、湿度、刮风,哪个作为根节点?
先了解两个指标:纯度和信息熵
先来说一下纯度。我们可以把决策树的构造过程理解成为寻找纯净划分的过程。数学上,我们可以用纯度来表示,纯度换一种方式来解释就是让目标变量的分歧最小
假设有3个集合
- 集合1 - 6次都去打篮球
- 集合2 - 4次去打篮球、2次没去打篮球
- 集合3 - 3次去打篮球、3次没去打篮球
所以,按照纯度来讲,集合1 > 集合2 > 集合3
我们再来了解下信息熵(shāng)的概念,英文为entropy,它表示了信息的不确定度。在信息论中,随机离散事件出现的概率存在着不确定性
为了衡量这种信息的不确定性,信息学之父香农引入了信息熵的概念,并给出了计算信息熵的数学公式
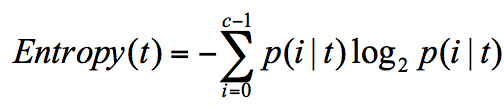
p(i|t)代表了节点t为分类i的概率,其中log2为取以2为底的对数
当不确定性越大时,它所包含的信息量也就越大,信息熵也就越高
假设有2个集合
- 集合1 - 5次都去打篮球、1次没去打篮球
- 集合2 - 3次去打篮球、3次没去打篮球
在集合1中,有6次决策,其中打篮球是5次,不打篮球是1次,那么假设:类别1为“打篮球”,即次数为5,类别2为“不打篮球”,即次数为1
那么节点划分为类别1的概率是5/6,为类别2的概率是1/6,带入上述信息熵公式可以计算得出:
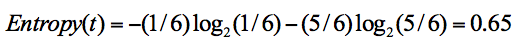
同样,集合2中,也是一共6次决策,其中类别1中“打篮球”的次数是3,类别2“不打篮球”的次数也是3,带入上述信息熵公式可以计算得出:
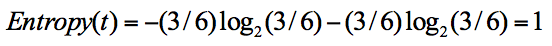
从上面的计算结果中可以看出,信息熵越大,纯度越低。当集合中的所有样本均匀混合时,信息熵最大,纯度最低
我们在构造决策树的时候,会基于纯度来构建。而经典的“不纯度”的指标有三种,分别是信息增益(ID3算法)、信息增益率(C4.5算法)以及基尼指数(Cart算法)
ID3算法
ID3算法计算的是信息增益,信息增益指的就是划分可以带来纯度的提高,信息熵的下降
它的计算公式是父节点的信息熵减去所有子节点的信息熵
在计算的过程中,我们会计算每个子节点的归一化信息熵,即按照每个子节点在父节点中出现的概率,来计算这些子节点的信息熵
所以信息增益的公式可以表示为:
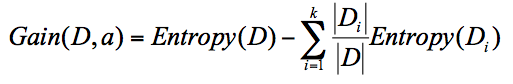
公式中D是父亲节点,Di是子节点,Gain(D,a)中的a作为D节点的属性选择
假设:天气=晴的时候,会有5次去打篮球,5次不打篮球。其中D1刮风=是,有2次打篮球,1次不打篮球
D2刮风=否,有3次打篮球,4次不打篮球。那么a代表节点的属性,即天气=晴
根据假设套用ID3公式,计算如下
$entropyD = -(1 / 2 * log(2, 1 / 2) + 1 / 2 * log(2, 1 / 2));
$entropyD1 = -(2 / 3 * log(2, 2 / 3) + 1 / 3 * log(2, 1 / 3));
$entropyD2 = -(3 / 7 * log(2, 3 / 7) + 4 / 7 * log(2, 4 / 7));
$gainDa = $entropyD - (3 / 10 * $entropyD1 + 7 / 10 * $entropyD2);
var_dump($gainDa);
现在我们回到训练集数据,基于ID3的算法规则,完整地计算下我们的训练集
import math
'''
先以天气作为属性划分,分为:晴天、阴天、小雨
我们以+号表示去打篮球,-号表示不去打篮球,如下:
D1(天气=晴天)={1-,2-,6+} # 第1行不打篮球、第2行不打篮球、第6行打篮球
D2(天气=阴天)={3+,7-} # 第3行去打篮球、第7行不打篮球
D3(天气=小雨)={4+,5-} # 第4行去打篮球、第5行不打篮球
'''
# 天气
entropyD = -(3 / 7 * math.log2(3 / 7) + 4 / 7 * math.log2(4 / 7))
entropyD1 = -(1 / 3 * math.log2(1 / 3) + 2 / 3 * math.log2(2 / 3))
entropyD2 = -(1 / 2 * math.log2(1 / 2) + 1 / 2 * math.log2(1 / 2))
entropyD3 = -(1 / 2 * math.log2(1 / 2) + 1 / 2 * math.log2(1 / 2))
gainDa = entropyD - (3 / 7 * entropyD1 + 2 / 7 * entropyD2 + 2 / 7 * entropyD3)
print(gainDa)
'''
同理我们再分别计算出温度、湿度、刮风为属性的根节点的信息增益
D1(温度=高)={1-,2-,3+,4+}
D2(温度=中)={6+,7-}
D3(温度=低)={5-}
D1(湿度=高)={3+,4+,5-,7-}
D2(湿度=中)={1-,2-,6+}
D1(刮风=是)={2-,6+,7-}
D2(刮风=否)={1-,3+,4+,5-}
'''
def entropy(data: list):
res = 0
for i in data:
res = res + i * math.log2(i)
return -1 * res
# 温度
entropyD1Temp = entropy([1 / 2, 1 / 2])
entropyD2Temp = entropy([1 / 2, 1 / 2])
entropyD3Temp = entropy([1])
gainDaTemp = entropyD - (4 / 7 * entropyD1Temp + 2 / 7 * entropyD2Temp + 1 / 7 * entropyD3Temp)
print(gainDaTemp)
# 湿度
entropyD1Hum = entropy([1 / 2, 1 / 2])
entropyD2Hum = entropy([2 / 3, 1 / 3])
gainDaHum = entropyD - (4 / 7 * entropyD1Hum + 3 / 7 * entropyD2Hum)
print(gainDaHum)
# 刮风
entropyD1Wind = entropy([2 / 3, 1 / 3])
entropyD2Wind = entropy([1 / 2, 1 / 2])
gainDaWind = entropyD - (3 / 7 * entropyD1Wind + 4 / 7 * entropyD2Wind)
print(gainDaWind)
通过计算,我们发现温度作为属性的信息增益最大
所以我们将信息增益最大的节点作为父节点,这样可以得到纯度高的决策树,所以我们将温度作为根节点
然后我们将第一个叶节点,也就是D1={1-,2-,3+,4+}进一步进行分裂,往下划分,计算其不同属性(天气、湿度、刮风)作为节点的信息增益
经过多轮计算,我们得到最终的决策树,如下图:

ID3的算法规则相对简单,可解释性强。同样也存在缺陷,比如我们会发现ID3算法倾向于选择取值比较多的属性
如果我们把“编号”作为一个属性(一般情况下不会这么做,这里只是举个例子),那么“编号”将会被选为最优属性
但实际上“编号”是无关属性的,它对“打篮球”的分类并没有太大作用
所以ID3有一个缺陷就是,有些属性可能对分类任务没有太大作用,但是他们仍然可能会被选为最优属性
这种缺陷不是每次都会发生,只是存在一定的概率。在大部分情况下,ID3都能生成不错的决策树分类
针对可能发生的缺陷,后人提出了新的算法进行改进,它就是大名鼎鼎的C4.5算法