多个随机变量之间的关系
对于现代的概率统计来说,分析多个随机变量之间的相互关系是一个关键
"包含'免费'这一单词的邮件很可能是广告"、"在星期五购买一次性纸尿布的顾客很可能也会买啤酒"这类观点是否很耳熟?
为了讨论这类问题,我们必须分析多个随机变量之间的相互关系
联合概率、边缘概率与条件概率这三个概念。它们是讨论随机变量之间关系的基本道具
最近活跃于各领域的贝叶斯公式也是这组概念的一种应用。此外,独立性的定义也基于这组概念
不过,为避免引入一些无关的复杂情况,本章将不涉及连续的随机变量(第4章将对此作具体说明)
不同县、不同用途的统计(联合概率与边缘概率的预热)
Ω国有3个县(A县、B县、C县),面积分别是P(A)、P(B)、P(C)。这些面积的和,即整个国家的总面积为1
P(A) + P(B) + P(C) = 1
这个国家的土地不是用于住宅或工厂,就是作为农田使用。我们假定这些用途的面积分别是P(住宅)、P(工厂)、P(农田),显然,整个国家的总面积仍然为1
P(住宅) + P(工厂) + P(农田) = 1
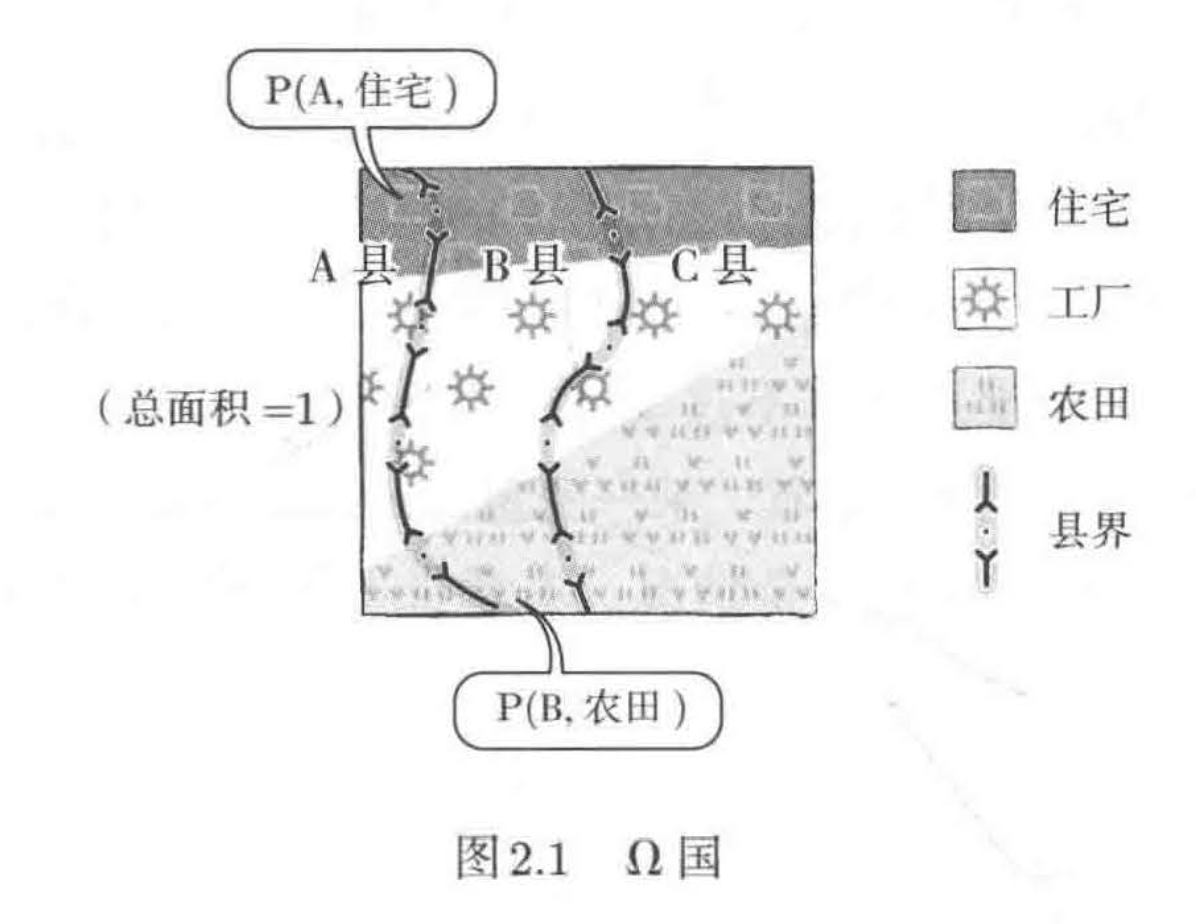
仅凭这些信息我们无法了解具体的土地使用情况,还需要调查A县的住宅面积P(A,住宅),B县的农田面积P(B,农田)。很明显,各县的住宅面积之和等于整个国家住宅的总面积
P(住宅) = P(A,住宅) + P(B,住宅) + P(C,住宅)
P(工厂) = P(A,工厂) + P(B,工厂) + P(C,工厂)
P(农田) = P(A,农田) + P(B,农田) + P(C,农田)
最后,这些面积之和应该与全国的总面积一致
P(A,住宅) + P(A,工厂) + P(A,农田) + P(B,住宅) + P(B,工厂) + P(B,农田) + P(C,住宅) + P(C,工厂) + P(C,农田) = 1
特定县、特定用途的比例(条件概率的预热)
与其他县相比,A县看似更重视工厂的发展。如果我们直接比较各县的工厂面积P(A,工厂)、P(B,工厂)及P(C,工厂),将无法获得正确的实际情况
在比较重视程度时,我们不应比较面积本身,而应比较该类型的面积在整个县内所占的比例
为此,我们可以使用P(工厂|A)来表示A县中工厂所占的比例,只需将"A县中工厂的面积"除以"A县的总面积"即可
P(住宅|A) = P(A,住宅)/P(A),P(工厂|A) = P(A,工厂)/P(A),P(农田|A) = P(A,农田)/P(A)
这些数值表示各自的比例,它们的和为1(不过这与整个国家的总面积1无关)
P(住宅|A) + P(工厂|A) + P(农田|A) = 1
此外,面积与比例之间存在以下关系
P(A,住宅) = P(住宅|A)P(A),P(A,工厂) = P(工厂|A)P(A),P(A,农田) = P(农田|A)P(A)
我们可以像下面这样分别计算比较各县中工厂所占的比例,以判断哪一个县更加重视工厂建设
P(工厂|A) = P(A,工厂)/P(A),P(工厂|B) = P(B,工厂)/P(B),P(工厂|C) = P(C,工厂)/P(C)
这里需要特别注意的是,下式的值并不一定为1
P(工厂|A) + P(工厂|B) + P(工厂|C)
而对于具体的某一个县来说,住宅、工厂与农田的比例之和为1
P(住宅|A) + P(工厂|A) + P(农田|A)
如果我们互换竖线两侧的值,新得到的P(A|工厂)表示所有工厂的总面积P(工厂)中A县工厂所占的比例
P(A|工厂) = P(A,工厂)/P(工厂)
倒推比例(贝叶斯公式的预热)
上一节已经强调过,P(用途|县)与P(县|用途)的含义不同。本节将讨论如何从一组P(用途|县)倒推出P(县|用途)的值
Ω国面积为1,有A、B、C3个县,分别如下:
- A县的总面积为0.2,B县的总面积为0.32,C县的总面积为0.48
- A县20%的土地用于住宅,60%用于工厂,20%用于农田
- B县50%的土地用于住宅,25%用于工厂,25%用于农田
- C县25%的土地用于住宅,25%用于工厂,50%用于农田
P(A,工厂) = P(工厂|A)P(A) = 60% * 0.2 = 0.12
P(B,工厂) = P(工厂|B)P(B) = 25% * 0.32 = 0.08
P(C,工厂) = P(工厂|C)P(C) = 25% * 0.48 = 0.12
P(工厂) = P(A,工厂) + P(B,工厂) + P(C,工厂) = 0.12 + 0.08 + 0.12 = 0.32
P(A|工厂) = P(A,工厂) / P(工厂) = 0.12 / 0.32 = 0.375
P(B|工厂) = P(B,工厂) / P(工厂) = 0.08 / 0.32 = 0.25
P(C|工厂) = P(C,工厂) / P(工厂) = 0.12 / 0.32 = 0.375
同理,我们可以分别求出ABC县的住宅和农田占全国住宅和农田的比例
比例相同的情况(独立性的预热)
我们假定各县中住宅、工厂与农田的比例完全相同,分别为:30%、20%、50%,则:
P(住宅|A) = P(住宅|B) = P(住宅|C)
P(工厂|A) = P(工厂|B) = P(工厂|C)
P(农田|A) = P(农田|B) = P(农田|C)
P(A,住宅) : P(A,工厂) : P(A,农田) = P(B,住宅) : P(B,工厂) : P(B,农田) = P(C,住宅) : P(C,工厂) : P(C,农田)
P(住宅|县) = P(住宅|Ω) = P(住宅)
P(工厂|县) = P(工厂|Ω) = P(工厂)
P(农田|县) = P(农田|Ω) = P(农田)
P(A,住宅) = P(住宅|A)P(A) = P(住宅)P(A),P(B,工厂) = P(工厂|B)P(B) = P(工厂)P(B)...
即:P(县,用途) = P(县)P(用途) = P(用途)P(县)
我们分别把A县的住宅、工厂、农田代入上面的公式
P(A,住宅) = P(A)P(住宅),而P(A|住宅) = P(A,住宅) / P(住宅),所以P(A|住宅) = P(A)P(住宅) / P(住宅) = P(A)
P(A,工厂) = P(A)P(工厂),而P(A|工厂) = P(A,工厂) / P(工厂),所以P(A|工厂) = P(A)P(工厂) / P(工厂) = P(A)
P(A,农田) = P(A)P(农田),而P(A|农田) = P(A,农田) / P(农田),所以P(A|农田) = P(A)P(农田) / P(农田) = P(A)
所以,P(A|住宅) = P(A|工厂) = P(A|农田) = P(A)
同理,P(B|住宅) = P(B|工厂) = P(B|农田) = P(B) 以及 P(C|住宅) = P(C|工厂) = P(C|农田) = P(C)
P(A)P(住宅) : P(B)P(住宅) : P(C)P(住宅) = P(A)P(工厂) : P(B)P(工厂) : P(C)P(工厂) = P(A)P(农田) : P(B)P(农田) : P(C)P(农田)
所以,P(A,住宅) : P(B,住宅) : P(C,住宅) = P(A,工厂) : P(B,工厂) : P(C,工厂) = P(A,农田) : P(B,农田) : P(C,农田)
预热总结
把"X"或"Y"或"X,Y"或"Y,X"归类为面积("X,Y"和"Y,X"等价),把"X|Y"或"Y|X"归类为比例("|"上方是"分子","|"下方是"分母")
在特殊场景下,"X"或"Y"也可以转换为比例,因为"X"或"Y"也可以表示成"X|Ω"或"Y|Ω",而Ω=1
| 公式 | 面积/比例 | 描述 |
|---|---|---|
| P(X) | 面积 | X县的面积 |
| P(X,工厂) | 面积 | X县中的工厂的面积 |
| P(工厂|X) | 比例 | X县中,土地用途为工厂的占比 |
| P(X|工厂) | 比例 | X县中的工厂占全国工厂的比列 |
联合概率与边缘概率
前面几节我们以"面积"和"比例"的形式进行了预热,本节起我们将它们转述为概率问题
假设有随机变量X与Y,此时,P(X=a,Y=b)用于表示X=a且Y=b的概率。这类包含多个条件且所有条件同时成立的概率称为联合概率
我们也可以用(a,b)来表示联合概率
联合概率并不是其中某个条件的成立概率,而是所有条件同时成立的概率
与之对应地,P(X=a)或P(Y=b)这类仅与单个随机变量有关的概率称为边缘概率
联合概率的一览表称为联合分布,边缘概率的一览表称为边缘分布
联合概率与边缘概率的关系如下:
表示"穷举Y可取的值b后,由所有与这些值对应的(...)相加得到的和"
表示"穷举X可取的值a后,由所有与这些值对应的(...)相加得到的和"
| 判断题 | 结果 |
|---|---|
| P(X=a,Y=b)=P(X=b,Y=a) | ❌ |
| P(X=a,Y=b)=P(Y=b,X=a) | ✅ |
| P(X=a,Y=b)=P(Y=a,X=b) | ❌ |
| O<=P(X=a,Y=b)<=P(X=a)<=1 | ✅ |
| P(X=a,Y=b)=1 | ❌ |
| P(X=a,Y=b)=1 | ✅ |
三个随机变量
为了讨论三个随机变量的情况,我们来重新分析一下蒙提霍尔问题
假设正确的门为X,挑战者选择的门为Y,主持人打开的门为Z。X、Y、Z都是随机变量,且值可能是1、2或3。X、Y、Z的联合分布如下表所示
| Y = 1 | Y = 2 | Y = 3 | |||||||
| Z = 1 | Z = 2 | Z = 3 | Z = 1 | Z = 2 | Z = 3 | Z = 1 | Z = 2 | Z = 3 | |
| X = 1 | 0 | 1/18 | 1/18 | 0 | 0 | 2/18 | 0 | 2/18 | 0 |
| X = 2 | 0 | 0 | 2/18 | 1/18 | 0 | 1/18 | 2/18 | 0 | 0 |
| X = 3 | 0 | 2/18 | 0 | 2/18 | 0 | 0 | 1/18 | 1/18 | 0 |
如果要求挑战者选择门3且主持人打开门1的概率,即边缘概率P(Y=3,Z=1),我们可以分别计算X值为1、2、3时的情况并将它们相加,如下所示:
P(Y=3,Z=1) = P(X=1,Y=3,Z=1) + P(X=2,Y=3,Z=1) + P(X=3,Y=3,Z=1) = 0 + 2/18 + 1/18 = 3/18 = 1/6
我们只要统计所有满足"Y=3且Z=1"的组合的出现概率,就能得到P(Y=3,Z=1)的值。在处理更多的随机变量时,该方法依然成立
那么,我们能否计算主持人打开门1的概率,即边缘概率P(Z=1)呢?根据上述方法,我们只需合计所有满足"Z=1"的组合的出现概率即可,如下所示
P(Z=1) = P(X=1,Y=1,Z=1) + P(X=1,Y=2,Z=1) + P(X=1,Y=3,Z=1) + P(X=2,Y=1,Z=1) + P(X=2,Y=2,Z=1) + P(X=2,Y=3,Z=1) + P(X=3,Y=1,Z=1) + P(X=3,Y=2,Z=1) + P(X=3,Y=3,Z=1)
P(Z=1) = 0 + 0 + 0 + 0 + 1/18 + 2/18 + 0 + 2/18 + 1/18 = 6/18 = 1/3
P(Y=3,Z=1)也是边缘概率吗?它使用了逗号,难道不是联合概率吗?
边缘概率是一个相对概念。对于随机变量X、Y、Z的联合分布来说,P(Y=3,Z=1)也是一种边缘概率。同时,P(Y=3,Z=1)也是Y=3与Z=1的联合概率
条件概率
在实际生活中,许多有价值的变量都能以条件概率这一概念来表述
本章开头提到了"包含'免费'这一单词的邮件很可能是广告",这种oo条件下事件xx的概率称为条件概率
我们以练习题2.1来讲解这一概念。扑克牌的花色及X、Y的联合分布如下所示
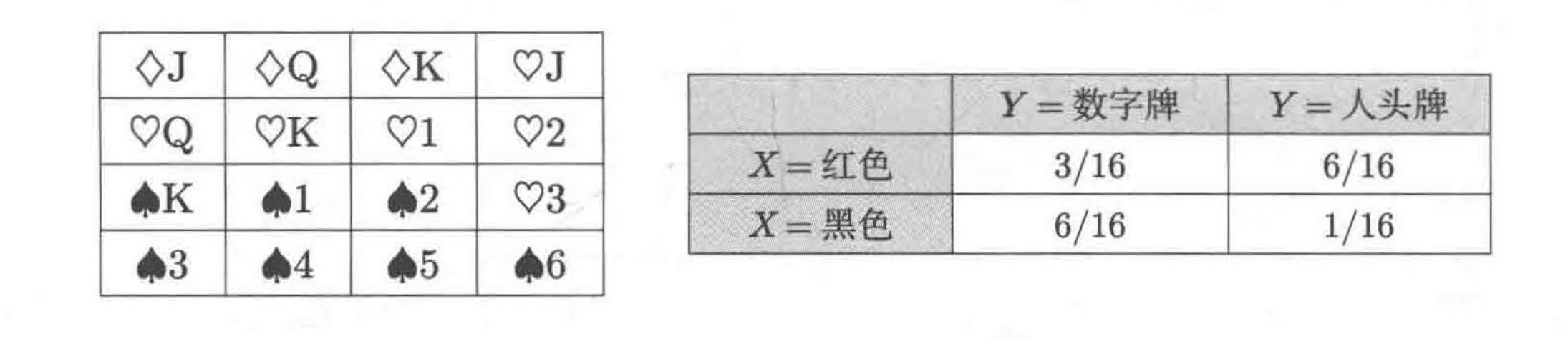
我们以"X=红色"为例。从上帝视角来看,"X=红色"的世界中有三分之一的"Y=数字牌",三分之二的"Y=人头牌"
P(Y=数字牌|X=红色) = 3/9 = 1/3
P(Y=人头牌|X=红色) = 6/9 = 2/3
即:P(Y=b|X=a)也可以写成
在条件X=红色成立时,Y=数字牌的条件概率是1/3
在条件X=红色成立时,Y=人头牌的条件概率是2/3
即:在条件X=红色下Y的条件分布
联合概率、边缘概率、条件概率的互换公式,如下:
a县中b的比例即是"a县中b的面积P(X=a,Y=b)"除以"a县的总面积P(X=a)"后得到的结果
P(Y=数字牌|X=红色) + P(Y=人头牌|X=红色) = 1
"在条件X=红色下Y的条件分布"也是一种"Y的概率分布",因此"穷举Y可取的值后,所有与这些值对应的概率之和为1"
不过,的值不一定为1
跟预热环节,所有县各自的工厂占比累加不一定等于1一致
如果P(X=a)=0,我们该怎样理解P(Y=b|X=a)昵?
本书将这种情况定义为无法确定,并将这种无法确定的0直接视作0
如果没有明确备注X = 0,都视为:X ≠ 0,否则有大量地方需要备注
联合分布、边缘分布与条件分布的关系
联合概率P(X=a,Y=b):满足X=a且Y=b的区域的面积,分母是:Ω
边缘概率P(X=a):不考虑Y的取值,所有满足X=a的区域的总面积,分母是:Ω
条件概率P(Y=b|X=a):在X=a的前提下,满足Y=b的区域的面积(比例),分母是:X=a
联合分布于边缘分布的关系如下:
P(X=a,Y=b) = P(X=a|Y=b)P(Y=b) = P(Y=b|X=a)P(X=a)
联合概率、条件概率的描述如下:
与ooxx同时成立时的联合概率P(oo,xx)
在oo的条件下事件xx的概率P(oo|xx)
现在有一副扑克牌,除去大王、小王后还剩52张。我们从中随机抽取一张,并将这张牌的颜色记为X。之后,我们再从剩余的51张中随机抽取一张牌,将它的颜色记为Y。试求X与Y为同一种颜色的概率
P(X和Y同一种颜色) = P(X=红色,Y=红色) + P(X=黑色,Y=黑色)
= P(Y=红色|X=红色)P(X=红色) + P(Y=黑色|X=黑色)P(X=黑色)
= 25/51 * 1/2 + 25/51 * 1/2 = 25/51
我们先确定了第一张牌的颜色X,按理说第二张牌的颜色Y的出现概率应该根据第一张牌的颜色结果调整
然后在计算X,Y的联合分布时,我们得到了完全对等的结果,如下图:
| Y = 红色 | Y = 黑色 | |
|---|---|---|
| X = 红色 | 25/102 | 26/102 |
| X = 黑色 | 26/102 | 25/102 |
由于联合分布是对等的,所以据此求得的边缘分布及条件分布都将对等。最终,我们无法从概率分布中得出因果关系
概率论最多只能处理X与Y之间的相互关系,而无法判断哪一个是原因,哪一个是结果
如果一定要区分原因与结果,该怎么办呢?
那我们就必须引入新的概念,因为单靠概率无法区分两者
一种方法是,引入时间的概念,从时间的角度来分析两个事件的前后关系
- 如果事件X先于事件Y发生,至少说明Y不是X的原因
- 而且,我们还要考虑下述可能,即"其实之前还存在一个没能观测到的事件A,A是事件X与Y的原因,X与Y都是A的结果"
- 即使"蛙呜翌日常落雨",青蛙的鸣叫声也不是降雨的原因
还有一种更明确的方法,即我们可以主动介入事件,而不是被动观测
- 如果X是Y的原因(X->Y),只要我们改变X,就能发现Y受到了影响
- 反之,如果X是Y的结果(Y->X),就算强制改变X,Y也不会离任何影响
练习题1
| 判断题 | 结果 |
|---|---|
| P(X=a|Y=b) = 1 | ❌ |
| P(X=a|Y=b) = 1 | ✅ |
| P(X=a|Y=b) = 1 | ❌ |
| P(X=a|Y=b) + P(Y=b|X=a) = 1 | ❌ |
| P(X=a|Y=b) = P(Y=b|X=a) | ❌ |
| P(X=a,Y=b) = P(X=a)P(Y=b) | ❌ |
| O <= P(X=a,Y=b) <= P(X=a|Y=b) <= 1 | ❌ |
| O <= P(X=a|Y=b) <= P(X=a) <= 1 | ✅ |
一、与B山相比,A山的P(发现松鼠,下雪)更高。同时,能否因此断言A山的P(发现松鼠)更高?
能。这是因为P(发现松鼠) = P(发现松鼠,下雪) + P(发现松鼠,不下雪)
备注:"发现松鼠并且下雪"的概率
二、与D山相比,C山的P(发现松鼠|下雪)更高。同时,能否因此断言C山的P(发现松鼠)更高?
不能。我们可以举出以下反例(辛普森悖论)
- C山:P(下雪) = 0.01,P(发现松鼠|下雪) = 0.8,P(发现松鼠|不下雪) = 0.1
- D山:P(下雪) = 0.99,P(发现松鼠|下雪) = 0.5,P(发现松鼠|不下雪) = 0
备注:"在下雪的时候,发现松鼠"的概率
三、对于E山,有以下事实。P(发现熊|下雪) < P(发现松鼠|下雪),P(发现熊|不下雪) < P(发现松鼠|不下雪),试问能否因此断言E山的P(发现熊)<P(发现松鼠)?
能。虽然跟第二题一样:"在下雪的时候,发现xx"的概率,但是本题是同一座"E山",下雪概率必定相同
- P(发现熊) = P(发现熊|下雪)P(下雪) + P(发现熊|不下雪)P(不下雪)
- P(发现松鼠) = P(发现松鼠|下雪)P(下雪) + P(发现松鼠|不下雪)P(不下雪)
备注:"在下雪的时候,发现熊"的概率,"在下雪的时候,发现松鼠"的概率
即使条件中使用的不是等号也一样适用
此前的章节我们都在讨论"某一指定值的概率",其实,这些理论对任意条件都适用
P(X<a,Y>b),X<a且Y>b的联合概率
P(X<a|Y>b),在Y>b的条件下X<a的条件概率
P(X<a) = P(X<a,Y<b) + P(X<a,Y=b) + P(X<a,Y>b)
P(X<a,Y>b) = P(X<a|Y>b)P(Y>b)
除了不等式,更复杂的条件也同样成立。例如,设骰子的点数为X,我们可以写出以下等式
P(X是偶数)
= P(X是素数,X是偶数) + P(X不是素数,X是偶数)
= P(X是偶数|X是素数)P(X是素数) + P(X是偶数|X不是素数)P(X不是素数)
= 1/3 * 1/2 + 2/3 * 1/2 = 1/2
用正式的术语来讲,上式中出现的是事件的联合概率与条件概率
例如,P(X是素数,X是偶数)是事件"X是素数"与"X是偶数"的联合概率
如果读者之前学过概率知识,比起随机变量,也许会更加熟悉事件的联合概率与条件概率
三个或更多的随机变量
"Y=b且Z=c"时,"X=a"的条件概率
P(X=a|Y=b,Z=c) = P(X=a,Y=b,Z=c) / P(Y=b,Z=c)
"Z=c"时,"X=a且Y=b"的条件概率
P(X=a,Y=b|Z=c) = P(X=a,Y=b,Z=c) / P(Z=c)
"Z=c且W=d"时,"X=a且Y=b"的条件概率
P(X=a,Y=b|Z=c,W=d) = P(X=a,Y=b,Z=c,W=d) / P(Z=c,W=d)
联合概率、边缘概率、条件概率转换
P(X=a,Y=b,Z=c) = P(X=a|Y=b,Z=c)P(Y=b,Z=c) = P(X=a|Y=b,Z=c)P(Y=b|Z=c)P(Z=c)
P(X=a,Y=b,Z=c) = P(Y=b|Z=c,X=a)P(Z=c,X=a) = P(Y=b|Z=c,X=a)P(Z=c|X=a)P(X=a)
...
P(X=a,Y=b,Z=c,W=d) = P(X=a|Y=b,Z=c,W=d)P(Y=b,Z=c,W=d)
= P(X=a|Y=b,Z=c,W=d)P(Y=b|Z=c,W=d)P(Z=c,W=d)
= P(X=a|Y=b,Z=c,W=d)P(Y=b|Z=c,W=d)P(Z=c|W=d)P(W=d)
...
P(X=a,Y=b|Z=c) = P(X=a|Y=b,Z=c)P(Y=b|Z=c)P(Z=c) / P(Z=c) = P(X=a|Y=b,Z=c)P(Y=b|Z=c)
...
P(U=u,V=v,W=w,X=x|Y=y,Z=z) = P(U=u,V=v|W=w,X=x,Y=y,Z=z)P(W=w|X=x,Y=y,Z=z)P(X=x|Y=y,Z=z)
式中每一个P都附有"Y=y,Z=z"的条件,也就是说,条件"Y=y,Z=z"是贯穿整个式子的大前提
因此,我们应首先声明这一前提,表示之后将基于这一大前提分解概率,而不必每次强调"Y=y,Z=z"
也就是说,可以"约分",即:
P(U=u,V=v,W=w,X=x) = P(U=u,V=v|W=w,X=x)P(W=w|X=x)P(X=x)
...
总结上面所有式子的规律
- 从右往左依次移动"|"
- 每次移动后累乘对应值
再议蒙提霍尔问题
我们再来回顾一下"三扇门问题"(蒙提霍尔问题)。现在,这个问题也可以通过联合概率与条件概率的概念来解释
设X是正确的门,Y是挑战者选择的门,Z是主持人打开的门。我们希望计算挑战者选择了门3且主持人打开了门1时,门3是正确答案时的条件概率,即P(X=3|Y=3,Z=1)的值
根据游戏规则,式中的联合概率需要按以下方式计算。由于X的值由骰子决定,因此我们能得到以下关系式
P(X = 1) = P(X = 2) = P(X = 3) = 1/3
Y是独立于X的随机变量,同样由骰子决定,并有以下关系
P(Y=3|X=1) = P(Y=3|X=2) = P(Y=3|X=3) = 1/3
主持人打开门Z的条件概率如下(主持人不能打开正确的门)
P(Z=1|X=1,Y=3) = 0
P(Z=1|X=2,Y=3) = 1
P(Z=1|X=3,Y=3) = 1/2
综上,我们将得到以下概率
P(X=3,Y=3,Z=1) = P(Z=1|X=3,Y=3)P(Y=3|X=3)P(X=3) = 1/2 * 1/3 * 1/3 = 1/18
P(X=2,Y=3,Z=1) = P(Z=1|X=2,Y=3)P(Y=3|X=2)P(X=2) = 1 * 1/3 * 1/3 = 1/9
P(X=1,Y=3,Z=1) = P(Z=1|X=1,Y=3)P(Y=3|X=1)P(X=1) = 0 * 1/3 * 1/3 = 0
综上所述
这就是如果挑战者坚持最初的选择,能够选中正确的门的概率。从该结果可以看出,改选另一扇门是更好的选择
P(X=2|Y=3,Z=1) = 1 - P(X=3|Y=3,Z=1) - P(X=1|Y=3,Z=1) = 1 - 1/3 - 0 = 2/3
条件联合概率的分解:
P(oo,xx|△△) = P(oo|xx,△△)P(xx|△△)
左侧 = P(oo,xx,△△) / P(△△),右侧 = (P(oo,xx,△△) / P(xx,△△)) * (P(xx,△△) / P(△△))
贝叶斯公式
本节将应用条件概率来解决逆问题。简单来讲,逆问题是指那些需要从结果反推原因的问题
与之相对的,从原因推结果的问题称为正问题。为便于理解,本节使用了原因、结果等词
尽管这些词简单易懂,但前面也说过,因果关系并不属于概率论的讨论范畴
但是有时候,原因X无法被直接观察、测量,所以我们还是需要通过其结果Y来反推原因X
- 通信:根据含有噪声的接收信号Y推测发送信号X
- 语音识别:根据麦克风识别的音频波形数据Y推测语音信息X
- 文字识别:根据扫描仪读取的图像数据Y推测用户书写的文字X
- 邮件自动过滤:根据收到的邮件文本Y推测邮件的类型X(是否是广告等)
注意:即使X相同,Y也可能不同。由于绝大多数情况中都存在噪声与误差,因此我们不能简单地使用函数Y=f(X)来模拟问题
为此,我们需要借助概率来处理这些噪声与误差,通过随机变量X、Y来表述X、Y之间的相互关系
练习题2
一、在某个角色扮演游戏中,玩家只要打倒怪物就能获得宝箱。宝箱有2/3的概率有陷阱。玩家虽然可以用魔法来检查陷阱,但这种判断方式并不完美,有1/4的错误概率
假设玩家打倒了怪物,获得了宝箱,并通过魔法判定该宝箱没有陷阱。请读者以此为前提,求"宝箱有陷阱"的概率
P(X=有陷阱) = 2/3
P(Y=没有发现|X=有陷阱) = 1/4
P(Y=发现了|X=没有陷阱) = 1/4
求:P(X=有陷阱|Y=没有发现) = ?
简单来讲,本节将讨论以下这种类型的问题
- 已知所有的P(原因)与P(结果|原因)一览
- 求:P(原因|结果)
在这类问题中,P(原因)称为先验概率,P(原因|结果)称为后验概率。相应的概率一览分别称为先验分布与后验分布。这些术语用于表现事件是发生于结果Y取得之前还是之后
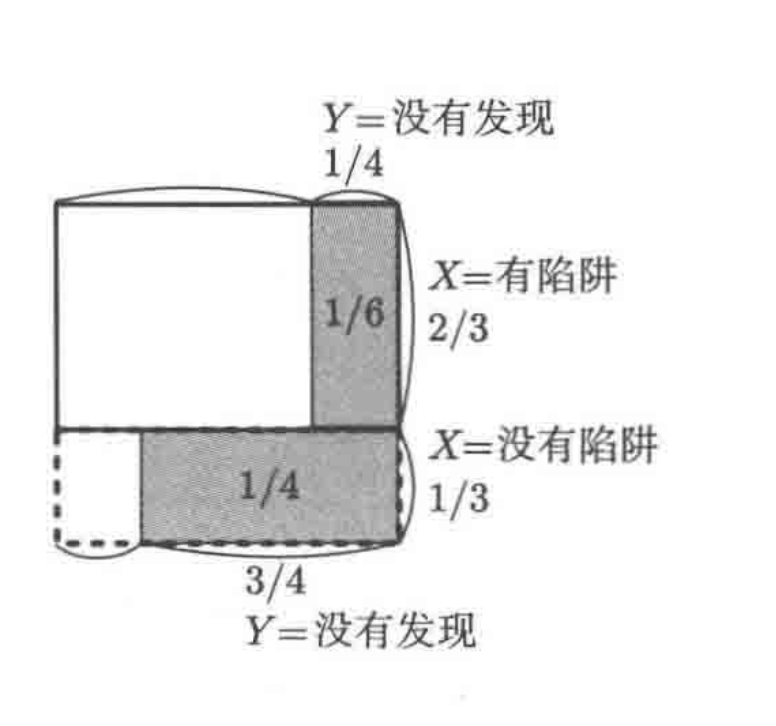
根据上图,我们可以计算出:P(Y=没有发现) = 2/3 * 1/4 + 1/3 * 3/4 = 5/12
而,P(X=有陷阱,Y=没有发现) = 2/3 * 1/4 = 2/12
所以,P(X=有陷阱|Y=没有发现) =
二、A市有10万人,其中有一个是外星人。我们现在有一台能够检验外星人的检测仪,不过它有1%的概率判断错误。也就是说,它有1%的可能性把外星人判断为人类,也有1%的可能性把人类误判为外星人
- 如果从10万人中随机抽取一人,检测仪有多大的概率将他判断为外星人?
- 从10万人中随机抽取一人后,检测仪将他判断为外星人,求这个人的确是外星人的概率
P(X=外,Y=外) = 1/10万 * 99/100 = 99 / 1000万
P(X=人,Y=外) = 99999/10万 * 1/100 = 99999 / 1000万
所以,P(Y=外) = 99 / 1000万 + 99999 / 1000万 = 100098 / 1000万(约等于0.1%)
所以,P(X=外|Y=外) = (约等于0.1%)
该检测仪看起来精度很高,因此我们很容易在仪器将检测对象判断为外星人时,相信他确实就是外星人
然而,从计算结果可知,这种情况的概率极低,后验概率仅为0.1%。这个例子告诉我们,在分析概率问题时,如果没有考虑先验概率,将很容易得到错误的结论
贝叶斯公式推导
已知的概率:P(X=原因)、P(Y=结果|X=原因)
需要求的条件概率:P(X=原因|Y=结果)
我们用a1、a2、a3、...、an代表原因,b代表结果
独立性
条件概率可以理解为在得知X后,对Y的出现概率的预测。贝叶斯公式是相应的逆运算,它将根据X->Y的情况(与X的先验概率分布),由Y逆推X的值
现在,我们重新开始讨论更为根本的问题。如果问题中存在多个随机变量,我们首先会怀疑这些随机变量之间是否真的存在关联。这一独立性的概念是很多应用问题中的关键
- 如果X与Y无关,由X推Y就没有意义。此时,Y与独立的X没有特别的含义
- 不过,独立的随机变量将带来一些好处。如果X与Y无关,我们就不必具体分析它们之间的关系,概率的计算将变得非常容易。我们甚至可以积极地利用独立性,将混有各种不同成分的信号分解为各种独立的成分以进一步求解(独立成分分析,independent component analysis,ICA)
- 通常,为了处理噪声与误差,我们需要反复进行相同的实验,记录实验的结果。如果先进行的实验对之后的实验存在影响,反复进行实验也没什么意义
不过,由于人们在日常中也会使用独立这个词,因此不少人都会误解概率论中独立性的含义。独立一词在词典中记载的解释与数学术语的定义不同
即使都是数学术语,线性独立中的独立与本章的独立也是不同的概念。下面再举一些容易误解的例子
"独立"与"均匀分布"不同,下面这样的关系并不是独立性
- P(Y=1|X=oo) = P(Y=2|X=oo) = P(Y=3|X=oo) = ...
"独立"与"(独立)同分布"不同,下面这样的关系并不是独立性
- P(X=1) = P(Y=1), P(X=2) = P(Y=2), P(X=3) = P(Y=3), ...
"独立"与"互斥"不同
- 独立性并不意味着"事件X=1与Y=1不会同时发生"。这种互斥性反而表示X与Y不是独立的随机变量。此时,我们能够通过X是1来确定Y不是1,因此,X与Y之间具有某些关联
概率论中的独立指的是X与Y没有任何关联。我们无法通过Y来判断X的值。也就是说,无论X是1、2还是3,Y的取值概率不变。接下来,我们将讨论如何通过数学表达式来表述这一性质
事件的独立性(定义)
我们回到宝箱陷阱检测问题。真正的魔法师能够通过魔法检测宝箱中是否有陷阱,只是准确性不够。而冒牌的魔法师根本不会检测,在检测时悄悄掷一下骰子,如果点数为1,则声称没有陷阱,否则声称有陷阱
显然,在这种情况下,"是否有陷阱"与"检测结果为存在陷阱"之间没有关联。条件概率能够充分展现这一事实。无论是否有陷阱,发现陷阱的条件概率不会改变
P(发现陷阱|有陷阱) = P(发现陷阱|没有陷阱) = 5/6
如果下面的关系成立,我们则称"oo与△△独立",准确来讲,应该是"事件oo与事件△△独立"
P(△△|oo) = P(△△|非oo)
在上例中,"有陷阱"与"检测结果为存在陷阱"相互独立。顺便一提,事件不独立称为"从属"或可直接称"不独立"(在P(oo)=0或在P(oo)=1时,尽管这一定义不再有意义,我们依然称oo与△△独立)
"oo独立于△△"的说法似乎更合适,"oo与△△独立"的说法不易区分两个事件的先后关系
- 我们无需区分两者,只要"oo独立于△△","△△独立于oo"也就自然成立
练习题3
一、现有一副不含大王、小王的扑克,共计52张。我们在洗牌后随机抽取一张,请问
- "这张牌是黑桃"与"这张牌是人头牌"是否独立?
- "这张牌是黑桃"与"这张牌是红桃"是否独立?
P(人头牌|黑桃) = 3/13,P(人头牌|不是黑桃) = 9/39 = 3/13。由于两值相等,所以两者独立
P(红桃|黑桃) = 0,P(红桃|不是黑桃) = 1/3。由于两值不相等,所以两者不独立
二、设掷骰子得到的结果为X
- "X能被3整除"与"X是偶数"是否独立?
- "X是素数"与"X是偶数"是否独立?
P(X是偶数|X能被3整除) = 3,6能被3整除,其中偶数是6,所以概率是1/2
P(X是偶数|X不能被3整除) = 1,2,4,5不能被3整除,其中偶数是2,4,所以概率是1/2
由于两值相等,所以"X能被3整除"与"X是偶数"独立
P(X是偶数|X是素数) = 2,3,5是素数,其中2是偶数,所以概率是1/3
P(X是偶数|X不是素数) = 1,4,6不是素数,其中4,6是偶数,所以概率是2/3
由于两值不相等,所以"X是素数"与"X是偶数"不独立
三、某魔法师的P(发现陷阱|有陷阱)=P(没发现陷阱|有陷阱)=1/2,他被怀疑是冒牌货。请为他辩护
我们无法根据题目中的条件判断"有陷阱"与"发现陷阱"是否独立。为此,我们必须知道P(发现陷阱|没有陷阱)的值。例如,如果P(发现陷阱|没有陷阱)=1/100,就说明"有陷阱"与"发现陷阱"不独立
独立的定义(多种等价表述方式)
独立的定义有多种等价表述方式,在讨论概率问题时,独立性是一种重要的基础概念,所以我们需要熟悉各种不同的表述方式
- oo与△△独立
- 条件概率与条件无关,P(△△|oo) = P(△△|非oo)
- 添加或去除条件不影响概率,P(△△|oo) = P(△△)
- 联合概率之比相同,P(oo,△△):P(oo,非△△) = P(非oo,△△):P(非oo,非△△)
- 联合概率是边缘概率的乘积,P(oo,△△) = P(oo)P(△△)
1、2是定义,3是2的变种,4的话,如下图:

我们再以上帝视角来看一下这些表述方式

- 第2条:"黑桃花色中人头牌所占的比例,与非黑桃花色中人头牌所占的比例相同"
- 第3条:"黑桃花色中人头牌所占的比例,与所有牌中人头牌所占的比例相同"
- 第4条:"黑桃花色中人头牌与非人头牌的比例,与非黑桃花色中人头牌与非人头牌的比例相同"
再来看一下第5条。在本例中,下面两个概率相同,体现了第5种表述的内涵
P(黑桃,人头牌) = 3/52,P(黑桃)P(人头牌) = 1/4 * 12/52 = 3/52
P(△△|oo) = P(△△,oo) / P(oo),根据第3条:P(△△|oo) = P(△△),可以推出:P(△△,oo) / P(oo) = P(△△),从而推出第5条
随机变量的独立性
我们已经讨论了事件的独立性,即"两种条件是否相互独立"。在此基础上,我们可以进一步讨论随机变量的独立性问题
如果无论a与b为何值,条件"X=a"与条件"Y=b"始终独立,我们称随机变量X与Y独立
- X与Y独立
- 条件概率与条件无关,P(Y=△|X=o)与o无关,仅由△确定
- 添加或去除条件不影响概率分布,无论△,o为何值,P(Y=△|X=o) = P(Y=△)始终成立
- 联合概率之比相同,无论o,x,△,口为何值,P(X=o,Y=△) : P(X=o,Y=口) = P(X=x,Y=△) : P(X=x,Y=口)始终成立
- 联合概率是边缘概率的乘积,无论o,△为何值,P(X=o,Y=△) = P(X=o)P(Y=△)始终成立
- 联合概率能够分解为仅含o的函数与仅含△的函数的乘积,即:P(X=o,Y=△) = g(o)h(△)(其中g与h是一元函数)
第6条是根据第5条推出的等价表述(因为g(o)只受o影响,h(△)只受△影响,而无论o,△为何值对事件的独立都没有影响)
如果联合分布以算式的形式出现,我们可以通过第6条方便地判断其中的随机变量是否独立
等式右边是"仅含a的表达式"与"仅含b的表达式(b+1)"的乘积。仅凭这点,我们就能确认X与Y相互独立
一、随机变量X,Y的联合分布如下表所示,请问X与Y是否独立?
| Y=o | Y=x | |
|---|---|---|
| X=壹 | 0.1 | 0.3 |
| X=贰 | 0.15 | 0.45 |
0.1 : 0.3 = 0.15 : 0.45,所以独立
二、相互独立的随机变量X、Y的边缘分布如下所示。请读者写出X、Y的所有联合概率
| X的值 | 该值的出现概率 | Y的值 | 该值的出现概率 |
|---|---|---|---|
| 壹 | 0.8 | o | 0.4 |
| 贰 | 0.2 | △ | 0.6 |
由于两者独立,因此边缘概率P(X=a)与P(Y=b)之积就是联合概率P(X=a,Y=b),因此,我们可以得到如下的联合概率表
| Y=o | Y=三角 | |
|---|---|---|
| X=壹 | 0.32 | 0.48 |
| X=贰 | 0.08 | 0.12 |
三个或更多随机变量的独立性
现有4张卡片,上面分别写有如下字样:-象人、蚁-人、蚁象-、---
如果我们随机抽取一张卡片,"写有蚁字"与"写有象字"这两个事件是独立的
- P(写有蚁字)P(写有象字) = 2/4 * 2/4 = 1/4 = P(写有蚁字,写有象字) = 1/4
- 或者P(写有象字|写有蚁字) = 1/2 = P(写有象字|没有蚁字) = 1/2
类似地,我们能够得到"写有象字与人字独立"或"写有人字与写有蚁字独立"
然而,我们不能说"蚁、象、人三个字的出现都相互独立"。例如,如果我们得知"卡片上写有蚁与象",就能断言"卡片上没有人字"
这表明,蚁、象与人这三个字的出现之间存在某种关联。如果没有关联,我们将无法从卡片上是否写有蚁字与象字推断出是否写有人字
从这个典型的例子中可以得出如下结论:各对事件相互独立不表示所有事件都相互独立
所以要证明oo,△△,口口独立的前提,是下面所有的情况都成立
P(oo|△△,口口) = P(oo),P(口口|oo,△△) = P(口口),P(△△|oo) = P(△△),P(△△|口口) = P(△△),...
用上面那种方式证明独立,要罗列的情况太多了,而且要考虑概率为0的情况,所以通常我们使用下面这种方式
P(oo,△△,口口) = P(oo)P(△△)P(口口),P(oo,△△) = P(oo)P(△△),P(oo,口口) = P(oo)P(口口),P(△△,口口) = P(△△)P(口口)
综上,要证明3个事件独立,需要证明2点
- 这3个事件本身的联合概率是边缘概率的乘积
- 其中任意2个事件相互独立
同理,要证明N个事件独立,需要证明2点
- 这N个事件本身的联合概率是边缘概率的乘积
- 其中任意N-1个事件相互独立
我们可以仅凭P(oo,△△,口口) = P(oo)P(△△)P(口口)断言"oo,△△,口口独立"吗
不能。例如,假设我们需要从下列8张卡片中随机抽取一张
o△口、o△-、o△-、o△-、--口、--口、--口、---
P(写有o,写有△,写有口) = 1/8 = P(写有o)P(写有△)P(写有口) = 1/2 1/2 1/2 = 1/8
但显然"写有o"与"写有△"这两个事件之间存在关联,并不独立
用变量的方式描述定义更简约(因为"无论a、b、c为何值"这一严格限制条件就能描述oo,△△,口口组合的各种情况)
如果无论a、b、c为何值,条件"x=a"、"Y=b"、"Z=c"始终独立,我们称随机变量X、Y、Z独立
如果随机变量X、Y,Z独立,以下表述也将成立
无论a、b、c为何值,P(x=a,Y=b,Z=c)=P(X=a)P(Y=b)P(Z=c)