程序员的数学2
《程序员的数学2》笔记
概率的定义
概率就是面积。概率论"舞台"的三元组:Ω、F、P,"主演":随机变量与概率分布
"F"应该是异体的,输入法打不出来,所以统一用"F"替代
蒙提霍尔问题
有三扇门,其中只有一扇是正确的门,打开后将能获得一辆高档豪车。另两扇门是错误选项,门内只有山羊。从门外无法获知哪一扇才是正确选项。挑战者需要从三扇门中选择一扇打开
在决定选择某扇门后,还剩两个选项,其中至少有一个是错误选择。此时,(知道正确答案的)主持人打开了没被选中的门中错误的那个,让挑战者确认了门后的山羊,并询问"是否要重新选择?"
挑战者是否应当重选,还是应该坚持最初的选择?又或是两种做法没有区别?
在挑战者做出第一次选择之后,有1/3的概率正确,2/3的概率不正确。无可争辩。那是否应该重新选择呢?
- 如果第一次选择正确,重选必定错误(因为剩下2个都是错误答案)
- 如果第一次选择错误,重选必定正确(因为知道答案的主持人会帮你排除掉那个错误选择)
也就是说,"第一次选择错误"的概率就是"重选后正确"的概率。重选的正确率是2/3,重选更加有利
飞艇视角表述
假设我们准备了大量游戏会场。在一个巨大的广场中分设了360个游戏会场,每个会场将同时进行游戏。你现在乘坐在飞艇中,从上空俯视这些会场
与之前的规则不同,我们这次为每个会场准备了剧本,主持人与挑战者都将按照剧本表演。所有人的行动都已事先确定。不过,每一个会场的剧本内容各不相同
我们将剧本设定为360个会场中有120个会场的门1是正确答案,120个会场的门2是正确答案,120个会场的门3是正确答案
在门1是正确答案的120个会场中,有40个会场的剧本要求挑战者选择门1,40个会场选择门2,40个会场选择门3
门2是正确答案的120个会场和门3是正确答案的120个会场也同样如此,如下图:
| 挑战者选择门1 | 挑战者选择门2 | 挑战者选择门3 | |
|---|---|---|---|
| 门1是正确答案 | ✅ 40个会场 | ❌ 40个会场 | ❌ 40个会场 |
| 门2是正确答案 | ❌ 40个会场 | ✅ 40个会场 | ❌ 40个会场 |
| 门3是正确答案 | ❌ 40个会场 | ❌ 40个会场 | ✅ 40个会场 |
之后,主持人将打开一扇错误的门。如果挑战者的选择错误,此时主持人只能打开错误的那扇门。如果挑战者的选择正确,剩下两扇门被主持人打开的概率各为一半
| 挑战者选择门1 | 挑战者选择门2 | 挑战者选择门3 | ||||
| 主持人 | 打开门2 | 打开门3 | 打开门1 | 打开门3 | 打开门1 | 打开门2 |
| 门1正确 | ✅ 20个会场 | ✅ 20个会场 | -- | ❌ 40个会场 | -- | ❌ 40个会场 |
| 门2正确 | -- | ❌ 40个会场 | ✅ 20个会场 | ✅ 20个会场 | ❌ 40个会场 | -- |
| 门3正确 | ❌ 40个会场 | -- | ❌ 40个会场 | -- | ✅ 20个会场 | ✅ 20个会场 |
通过飞艇视角,我们能更直观的看出重选的正确率是2/3,甚至可以数出之前的轻率结论究竟错了几处
比如:挑战者选择了门3而主持人打开了门1的会场共有60个。其中,门3是正确答案的会场仅有20个
这种方式的优势十分明显。如果我们通过直觉来说明概率这种抽象的概念,往往很难把问题解释清楚。如果换用飞艇视角,抽象的情况就被转换为了具体的统计问题
- 准备了大量会场,每个会场将会同时进行游戏
- 在各个会场中,所有人仅仅是按照事先确定的剧本行动
- 只要剧本设定合理,整个广场中所有会场的结果能够完美模拟原本的事件发生概率
- 只要从飞艇上俯瞰并统计会场的数量,就能明确判断各种结论的正误
三元组(Ω、F、P)之上帝视角
我们把会场理解成"世界",上帝能够置身各种平行世界之外俯视着它们
每个世界都会预先准备专用的剧本。剧本中记录了某个世界从古至今乃至未来发生的所有事件
无论是什么,一切都只是根据剧本发展而已。对于某个特定的世界来说,所有的结果都已确定,不存在任何随机事件
但是人类并不知道自己住在哪个世界,从人类的视角看,所有的事件都是随机的

习惯上,我们会以希腊字母ω来表示具体每一个世界。与之对应的所有平行世界组成的集合由大写的Ω表示
Ω的子集A(如果不习惯这个词,可以理解为Ω内的区域A)的面积将由P(A)表示
用于表示面积的函数P是(Ω、F、P)的第三个元素。对于所有平行世界P(A)=1,这是前提条件。第二个元素F不太容易理解,这里暂且跳过
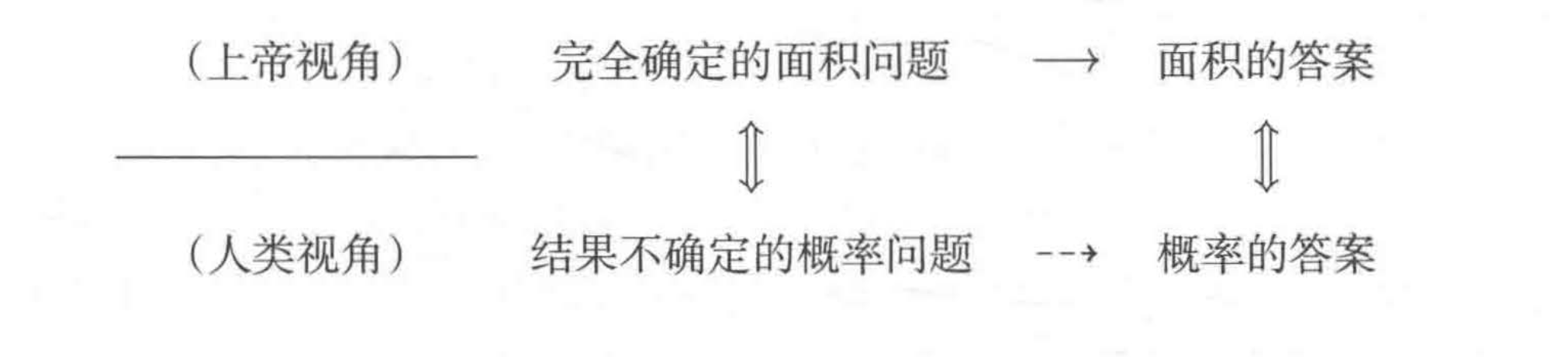
最终我们可以得到以下结论:只要知道由所有平行世界组成的集合Ω与用于测量Ω中区域面积的函数P,就能对概率问题进行讨论
借助这两个元素,概率问题被转换为了"区域与面积"的问题。这种方式的特点在于,不确定的概率问题成为了确定的数学问题
概率的概念不够直观,在将它转为面积这样含义清晰的值之后,我们就可以进一步展开明确的讨论
随机变量
随机变量从上帝视角看就是一个函数:f(ω),习惯上,我们会通过X(ω)这样的大写字母来表示随机变量
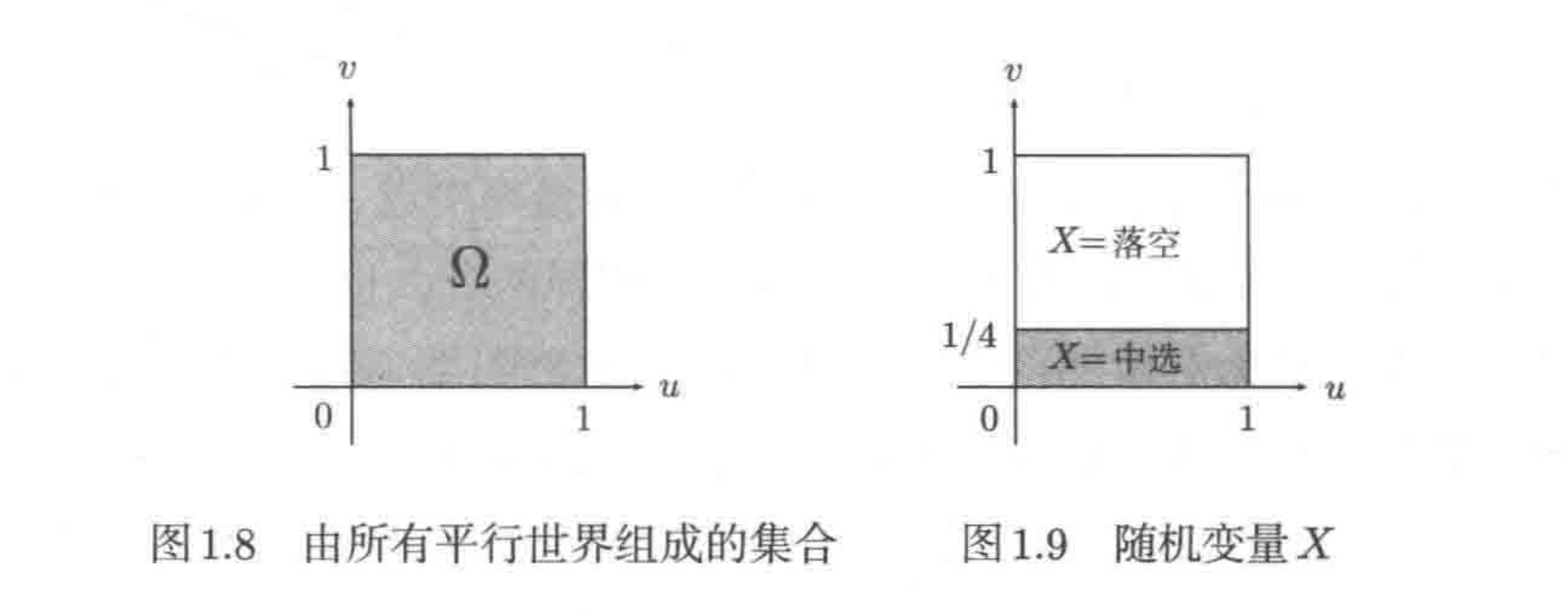
如图1.8所示,Ω是一个正方形。从集合的角度来讲,它是一个由0至1间的实数组成的二元组集合。也就是说,Ω中的元素呈ω=(u,v)的形式(0<=u<=1且0<=v<=1)。P是传统意义上的面积。整个Ω的面积为1
我们将按照图1.9来定义随机变量X
随机变量X的值是中选与落空这两种选项之一。这类既非整数又非实数的值也能作为随机变量定义。例如,对于ω=(0.3,0.5),则X(0.3,0.5)=落空
而对于ω=(0.2,0.1),则X(0.2,0.1)=中选。那么,X的值为中选的概率是多少呢?由于X=中选对应的面积是1/4,因此X有1/4的概率值为中选
为帮助理解,我们再来看一下另一个随机变量的例子
由图1.10可知,Y有1/4的概率中选,3/4的概率落空
区域的边界就是一条直线
2u + v = 1
v = -2u + 1
斜率为-2,y轴截距为1(当u=0),x轴截距为0(当v=0)
S = 1/2 * 1 / 2 = 1/4
最后,我们再看一个实数值的随机变量
- Z的取值范围是什么?
- Z大于等于O且小于等于10的概率是多少?
对于第一个问题,根据u与v的范围可知,Z可以是-20(u=0,v=1)至20之间的实数(u=1,v=0)
对于第二个问题,如图1.11所示,当Z(u,v)<=10时,(u,v)表示的面积为3/8(1/2-1/8)
区域的边界是两条直线
20u - 20v = 10 或 20u - 20v = 0
v = u + 1/2 或 v = u
S = (1 * 1) - (1 * 1 / 2) - (1/2 * 1/2 / 2) = 1/4

对于以整数或实数为对象的随机变量X与Y,我们只要通过直观的方式来理解X+1、3X、X+Y,或XY等表达式的含义即可
从普通人的视角看来,"随机值X"加上1后得到的就是X+1。从上帝视角来看,X+1表示的是各个世界中值为X(ω)+1的函数
概率分布
随机变量涉及具体的平行世界。与之相对地,概率分布的概念更为宽泛,它只考虑面积,不涉及具体的平行世界。在不会产生歧义时,我们可以将概率分布简称为分布
两种表述方式没有本质区别,我们需要注意的是概率分布与随机变量之间的差异。对于随机变量,哪一个世界中将得到哪一个值都已确定,而概率分布不涉及事件具体发生在哪一个世界
概率分布表达式:
下面的写法含义相同:
下面的表达式表示"X为k的概率"
P(X=k) = "X(ω)=k时区域ω的面积"
只要得到随机变量X,我们就能求出相应的概率分布,但反过来却不成立,仅凭概率分布,我们无法求出随机变量的值
概率分布的2条性质,如下:
- 每一项概率都大于等于O且小于等于1
- 所有概率的和必定为1
从上面采用的面积的角度来看,这是理所应当的两条性质(在集合Ω面积为1的前提下)
不过,即使没有列出所有的公式,我们只要知道了所有值的出现概率,就能表述概率分布
P(X=k) = 12/25k (其中k=1,2,3,4) (1.4)
此时,与其说"式1.4是随机变量X的概率分布",不如说"随机变量X遵从式1.4中的概率分布"
随机变量和概率的表述方式(简写)
有时,为了图省事,人们也会对随机变量进行简写,所以我们必须根据上下文判断该字母究竟表示哪种含义
X(ω) = a 可以简写为:X(ω) 甚至:X
P(2<=X<=7)表示概率P(A),其中A是"由所有满足2<=X(ω)<=7的ω组成的集合"
同理,对于P(X=3)表示的概率P(A),集合A是"由所有满足X(ω)=3的ω组成的集合"
我们有时也会将P(X=3)改写为Px(3)的形式。如果不会产生歧义,我们还可以进一步省略,只写出P(3)
同时存在两个随机变量X与Y时,我们应该怎样区分表示它们各自的概率分布。P(X=3)或Px(3)的写法虽然稳妥,但如果数量过多也容易看花眼,书写也比较麻烦
我们也可以这样写:"将X的概率分布记为P,Y的概率分布记为Q"。此时,P(3)表示P(X=3),Q(3)表示P(Y=3)。这种方式的优点是不必使用下标,书写更加方便,但也有需要引人新字母的不足
在实际使用中,我们有时还会使用更加简略的表示方法。那就是可以将P(X=x)简记为P(x),P(Y=y)则可以简记为P(y)。对于没有上下文的P(3),我们将无法辨别它的具体含义
有时还会使用Pr(...)或Prob(...)等写法代替P。它们的含义相同
一些内容较浅的概率论书籍常会采用这种方式。例如,试考虑投掷一次硬币的情况,我们只需将Ω设定为仅有两个元素的集合{正面,反面}即可
其中∅表示空集{}。P(∅)=0,P({正面})=1/2,P({反面})=1/2,P({正面,反面})=p(n)=1
解释
本书是一本主要给非数学专业的人阅读的概率统计相关入门数据,所以不涉及测度理论及概率论公理,也不涉及面积的定义