程序员的数学

《程序员的数学》笔记

0的故事

0不单单表示没有的意思，还有很多其他作用

  • 占位 如：2503中的0
  • 统一标准，简化规则 如：10010^0可以将按位计数法的各个数位所对应的大小统一表示成10n10^n

按位计数法

N进制计数法，使用的数字有0,1,2,3,...,N-1，共N种

从右往左分别为N0N^0的位、N1N^1的位、N2N^2的位、N3N^3的位...（基数是N）

例如，N进制计数法中，4位数a3a2a1a0a_3a_2a_1a_0为：

a3×N3+a2×N2+a1×+N1+a0×N0a_3 \times N^3 + a_2 \times N^2 + a_1 \times + N^1 + a_0 \times N^0（a3a_3、a2a_2、a1a_1、a0a_0是0~N-1中的数字）

十进制的按位计数法可以用以下表达式表示：

an×10n+an−1×10n−1+an−2×10n−2a_n \times 10^n + a_{n-1} \times 10^{n-1} + a_{n-2} \times 10^{n-2} + ... + a2×102+a1×101+a0×100a_2 \times 10^2 + a_1 \times 10^1 + a_0 \times 10^0

按位计数法的各个数位也能统一写作：

ak×10ka_k \times 10^k

指数法则

Na×Nb=Na+b N^a \times N^b = N^{a+b} \quad （N ≠ 0）

逻辑

编程中的逻辑表达式

数轴法、文氏图、真值表、电路图（异或逻辑等）、卡诺图（简化逻辑表达式、设计逻辑电路等）

逻辑非 ￢A 也可记作 A‾\overline A 双重否定 ￢￢A

逻辑与 A ∧ B

逻辑或 A ∨ B

异或 A ⊕ B

相等 A = B 也可记作 A ≡ B 若A为true，则B也为true。若A为false，则B也为false

蕴涵 A => B 若A为true，则B也为true。若A为false，则B为true或false都可以

蕴涵的逆否命题必定与其相等 A => B 等于 (￢B) => (￢A)

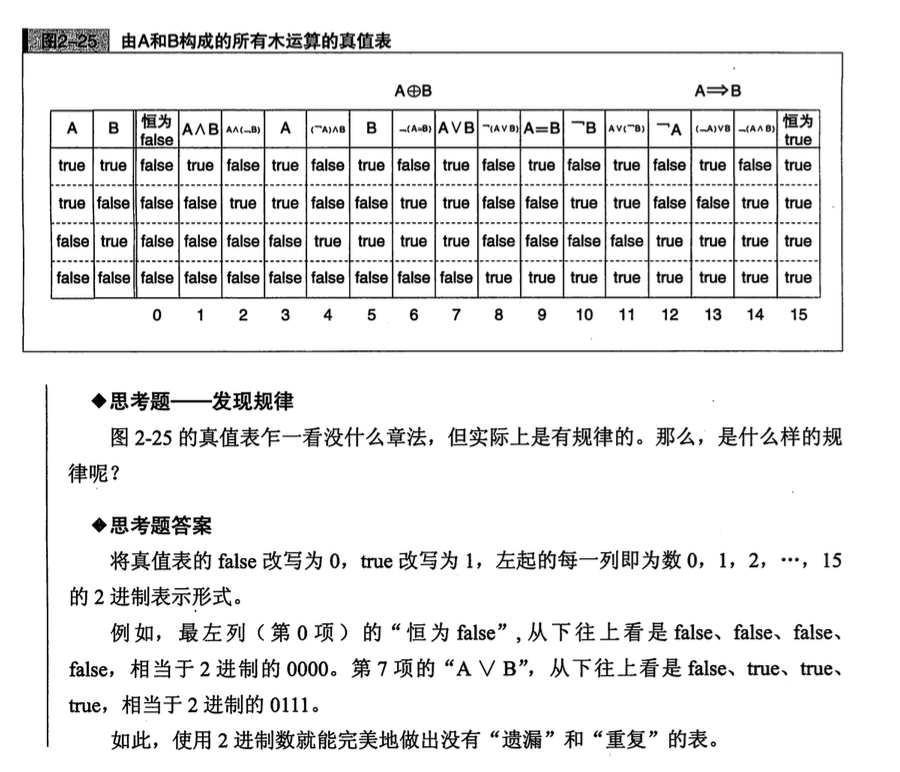
由A和B构成的所有逻辑运算的真值表

德·摩根定律，运用对偶性来灵活地转换逻辑表达式（true<->false、A<->￢A、∧<->∨）

(￢A) ∨ (￢B) = ￢(A ∧ B) "非A" 或者 "非B"，和非"A与B"是等价的

(￢A) ∧ (￢B) = ￢(A ∨ B) "非A" 并且 "非B"，和非"A或B"是等价的

余数

"余数就是分组"，有时运用余数恰当地分组（找规律）可以轻松解决难题

跟余数有关的奇偶性可用于检查通信错误，是个很重要的概念

  • 黑白棋通信（棋盘被动过，奇偶互换）
  • 奇偶村（奇数步能到达的村庄和偶数步能到达的村庄）
  • 铺草席问题（把半张草席涂黑另外半张涂白，黑色+1，白色-1，不为0则不能铺满整个房间，但是：为0也不能代表能铺满，逆命题不一定为真）
  • 一笔画问题（抽象成图，奇数点为单通道（包括来回来...），偶数点为双通道（包括来回来回...）。起点相同：所有点为偶数点；起点不同：起点、终点为奇数点，其他全为偶数点）

数学归纳法

数学归纳法是证明有关整数的断言对于0以上的所有整数（0,1,2,3...n）是否成立时所用的方法

  1. 证明P(0)成立。我们把步骤1称为基底
  2. 证明不论k为0以上的任何整数，若P(k)成立，则P(k+1)也成立。我们把步骤2称为归纳

高斯求和，证明0到n的整数和与n×(n+1)2\frac{n \times (n+1) }{2}相等

步骤1：基底的证明

G(0)为：0×(0+1)2=0\frac{0 \times (0+1) }{2} = 0，成立

步骤2：归纳的证明

G(k)为：k×(k+1)2\frac{k \times (k+1) }{2}

G(k+1)为：(k+1)×(k+1+1)2\frac{(k+1) \times (k+1+1) }{2}

G(k+1)又等于G(k)+k+1

所以，G(k+1)为：k×(k+1)2+k+1\frac{k \times (k+1) }{2} + k + 1

将k+1转换成分式：k×(k+1)2+2×(k+1)2\frac{k \times (k+1) }{2} + \frac{2 \times (k+1) }{2}

相加：k×(k+1)+2×(k+1)2\frac{k \times (k+1) + 2 \times (k+1)}{2}

合并同类项：(k+1)×(k+2)2\frac{(k+1) \times (k+2)}{2} 与 G(k+1) 相等

所以，高斯求和公式成立

排列组合

排列组合是解决计数问题的一种方法

计数问题必须要注意"遗漏"和"重复"

植树问题：10米的马路上每隔1米种一棵树，一共种多少棵树，11棵（0也要考虑进去）。抽象化后就是n米为n+1棵

加法法则

A ∪ B 的元素数 = A的元素数 + B的元素数，记作：|A ∪ B| = |A| + |B|（只在集合中没有重复元素的条件下成立）

容斥原理，当集合中存在重复元素的时候，需要减去重复元素的个数

|A ∪ B| = |A| + |B| - |A ∩ B|

乘法法则

从集合A和集合B中各取出一个元素作为一组，所有这种组合的集合为：A × B，记作：|A × B| = |A| × |B|

32个灯泡：1个灯泡有亮灭2种状态，2个灯泡有2×2种状态，3个灯泡有2×2×2种状态，所以：32个灯泡有2322^{32}种状态

置换

ABC三张牌按照ABC、ACB、BAC、BCA、CAB、CBA的顺序排列，共6种情况

将n个事物按顺序进行排列称为置换

第1张牌有3种选法、第2张牌有2种选法、第3张牌有1种选法，即：3 × 2 × 1 = 6

阶乘

ABCDE五张牌的置换计算为：5 × 4 × 3 × 2 × 1 = 120

可以用5!表示，称为5的阶乘

排列

置换是罗列n个事物的所有排法，而从n个事物中取出部分进行排列的排法称为"排列"

从ABCDE五张牌中选取三张进行排列：5 × 4 × 3 = 60

从n张牌中取出k张进行排列的总数可以归纳为：

PnkP_n^k = n × (n-1) × (n-2) × ... × (n-k+1)

如果把n记为：n-0，n-k+1记为：n-(k-1)，则归纳为：

PnkP_n^k = (n-0) × (n-1) × (n-2) × ... × (n-(k-1))

P50P_5^0被定义为1而不是0。因为从5张牌中选取0张的情况只有一种，就是不选取

置换是特殊的排列，可以记作：PnnP_n^n

排列也可以用阶乘表示，分母和分子可以约分

Pnk=n!(n−k)!P_n^k = \frac{n!}{(n-k)!}

组合

置换和排列都需要考虑顺序，而组合不需要考虑顺序

要计算ABCDE五张牌里面取三张的组合总数，只要这样考虑就行了

  1. 和排列一样"考虑顺序"进行计数
  2. 除以重复计数的部分（重复度）

假设选取的3张牌分别是：A、B、C，可以组成：ABC、ACB、BAC、BCA、CAB、CBA六种情况

所以，重复度就是被选取的3张牌的置换：P33=6P_3^3 = 6

C53=P53P33C_5^3 = \frac{P_5^3}{P_3^3}

Cnk=PnkPkkC_n^k = \frac{P_n^k}{P_k^k}

Cnk=n!(n−k)!k!C_n^k = \frac{ \frac{n!}{(n-k)!} }{k!}

Cnk=n!(n−k)!×1k!C_n^k = \frac{n!}{(n-k)!} \times \frac{1}{k!}

Cnk=n!(n−k)!×k!C_n^k = \frac{n!}{(n-k)! \times k!}

思考题

一、假设要将A、B、C三种药品调剂成一种新药，规则如下：

  1. 从A、B、C三种药品中，共取100粒进行调剂
  2. 调剂时，A、B、C三种药品每种至少出现一次
  3. 不考虑药品调剂的顺序
  4. 同种药品每粒都相同

我们假设100粒药品放在100个托盘上面，中间用隔板隔开

那么中间有99个位置可以插隔板

根据已知条件②③④，我们可以插入2块隔板。第一块隔板前放A，两块隔板中间放B，第二块隔板后面放C

即：从99个插槽处任意两处插入隔板

C992=99×982×1=4851C_{99}^2 = \frac{99 \times 98}{2 \times 1} = 4851

归纳为：Cn−1k−1C_{n-1}^{k-1}

二、5张扑克牌，其中王牌2张，J、Q、K各1张。将5张牌排成一排，左端或右端至少有一端是王牌的排法有多少种？（不区分大小王）

解法1：

左端是王牌 + 右端是王牌 - 两端是王牌（容斥原理）/ 王牌的重复度（不区分大小王）

P21×P44+P21×P44−P22×P33P22\frac{P_2^1 \times P_4^4 + P_2^1 \times P_4^4 - P_2^2 \times P_3^3}{P_2^2}

2×24+2×24−2×62=42\frac{2 \times 24 + 2 \times 24 - 2 \times 6}{2} = 42

解法2：

使用逻辑的解法，"至少有一端是王牌"也就是"两端都不是王牌"的否定，也就是说："所有的排列法"减去"两端都不是王牌"即可

所有的排列 - 两端不是王牌 / 王牌的重复度（不区分大小王）

P55−P32×P33P22\frac{P_5^5 - P_3^2 \times P_3^3}{P_2^2}

120−6×62=42\frac{120 - 6 \times 6}{2} = 42

递归

递归的思维方式：能将复杂问题转换为较为简单的同类问题吗？

在问题中找出递归结构，找出同类的简单问题，并将它当做"已知条件"，建立递推公式

如果在递推公式的基础上找出解析式，那是更好的，如果找不到，只建立递推公式也是非常有用的

汉诺塔

汉诺塔的解题思路，借助目标柱将n-1层圆盘移动到中转柱，然后把最大的圆盘移动到目标柱，再借助起点柱将n-1层圆盘移动到目标柱

以上步骤可知，为了解出n层汉诺塔，需要使用n-1层汉诺塔的解法，然后使用递归，直到0层

n层汉诺塔的移动次数 = n-1层汉诺塔的移动次数 + 移动最大的圆盘次数 + n-1层汉诺塔的移动次数

递归结构：H(n) = H(n-1) + 1 + H(n-1)

同类的简单问题：H(0)=0

根据递归结构和同类简单问题，建立递推公式

H(n)={0(n=0)H(n−1)+1+H(n−1)(n=1,2,3...)H(n) = \begin{cases} 0 \quad \quad (n=0)\\ H(n-1)+1+H(n-1) \quad \quad (n=1,2,3...) \end{cases}

H(0)=0

H(1)=H(0)+1+H(0)=0+1+0=1

H(2)=H(1)+1+H(1)=1+1+1=3

H(3)=H(2)+1+H(2)=3+1+3=7

H(4)=H(3)+1+H(3)=7+1+7=15

H(5)=H(4)+1+H(4)=15+1+15=31

H(6)=H(5)+1+H(5)=31+1+31=63

根据上面公式，可以找到规律，即：H(n)=2n−1H(n)=2^n-1

这种只使用n表示H(n)的式子叫做解析式，可以用数学归纳法来证明解析式的正确性

汉诺塔移动步骤

def hanoi(n, x, y, z):
    if n == 0:
        pass
    if n == 1:
        # hanoi(2 - 1, x, z, y)、hanoi(1, x, y, z)、hanoi(2 - 1, z, y, x)都会在这里输出
        print("{}->{}，".format(x, y))
    else:
        # 将n-1层汉诺塔从起点柱移动到中转柱，借助目标柱
        hanoi(n - 1, x, z, y)
        # 移动最大的圆盘，从起点柱到目标柱
        hanoi(1, x, y, z)
        # 将n-1层汉诺塔从中转柱移动到目标柱，借助起点柱
        hanoi(n - 1, z, y, x)

hanoi(6, 'A', 'B', 'C')

汉诺塔移动次数

def hanoiTimes(n):
    if n == 0:
        return 0
    else:
        return hanoiTimes(n - 1) + 1 + hanoiTimes(n - 1)

print(hanoiTimes(0))
print(hanoiTimes(1))
print(hanoiTimes(2))
print(hanoiTimes(3))
print(hanoiTimes(4))
print(hanoiTimes(5))
print(hanoiTimes(6))

阶乘

递归结构：n ≠ n * (n-1)!

同类的简单问题：0 ≠ 1

根据递归结构和同类简单问题，建立递推公式

n ≠ {1(n=0)n×(n−1)!(n=1,2,3...)\begin{cases} 1 \quad \quad (n=0)\\ n \times (n-1)! \quad \quad (n=1,2,3...) \end{cases} 

def factorial(n):
    if n <= 1:
        return 1
    else:
        return n * factorial(n - 1)


print(factorial(1))
print(factorial(2))
print(factorial(3))
print(factorial(4))
print(factorial(5))

递归和归纳

递归（recursion）和归纳（induction）本质上是相同的，都是"将复杂的问题简单化"

递归和归纳只是方向不同

递归的思想：从一般性前提推出个别性结论

归纳的思想：从个别性前提推出一般性结论

斐波那契数列

F(n)={0(n=0)1(n=1)n×F(n−1)+F(n−2)(n=2,3,4...)F(n) = \begin{cases} 0 \quad \quad (n=0)\\ 1 \quad \quad (n=1)\\ n \times F(n-1)+F(n-2) \quad \quad (n=2,3,4...) \end{cases}

杨辉三角形

n表示第几个数字，k表示层数（每层的总个数等于层数）

当前数字 = 上一层的左边那个数字(index - 1) + 上一层的右边那个数字(index与之相等)

F(n)={1(n=1∣k)F(n−1,k−1)+F(n,k−1)(1<n<k)F(n) = \begin{cases} 1 \quad \quad (n = 1 | k)\\ F(n-1,k-1)+F(n,k-1) \quad \quad (1 < n < k) \end{cases} 

def YangHui(n, k):
    if n < 1 or n > k:
        raise BaseException('0<n<k')
    if n == 1 or n == k:
        return 1
    else:
        return YangHui(n - 1, k - 1) + YangHui(n, k - 1)

print(YangHui(1, 6))
print(YangHui(2, 6))
print(YangHui(3, 6))
print(YangHui(4, 6))
print(YangHui(5, 6))
print(YangHui(6, 6))

海龟作图

海龟作图的4个关键步骤

  • forward(n)，前进n步并画线
  • back(n)，后退n步不画线
  • left()，左转一定的角度
  • right()，右转一定的角度

使用海龟作图画二叉树

def drawTree(n):
    if n == 0:
        pass
    else:
        left()
        forward(n)
        drawTree(n - 1)
        back(n)
        right()

        right()
        forward(n)
        drawTree(n - 1)
        back(n)
        left()


def left():
    print('左转45度')


def right():
    print('右转45度')


def forward(n):
    print('向前{}步并画树枝'.format(n))


def back(n):
    print('后退{}步'.format(n))


drawTree(3)

指数爆炸

2n2^n会产生指数爆炸，n2n^2不会产生指数爆炸

折纸问题、汉诺塔、斐波那契数列等都会产生指数爆炸

没有处理好指数爆炸，会膨胀到难以收拾的地步。相反，巧妙利用指数爆炸，它将成为解决难题的利器

如果问题中存在指数爆炸，我们就不能使用"一个不漏"的方法解决

二分法、对数、密钥等都是巧妙利用指数爆炸的经典算法或场景

列1 列2
105=10000010^5 = 100000 log10100000=5 \log_{10}^{\quad 100000} = 5
log10103=3\log_{10}^{\quad 10^3} = 3 log1010n=n \log_{10}^{\quad 10^n} = n
10log101000=100010^{\log_{10}^{\quad 1000}} = 1000 10log10n=n 10^{\log_{10}^{\quad n}} = n
10x×10y=10x+y10^x \times 10^y = 10^{x + y} log10x×y=log10x+log10y(x>0,y>0) \log{10}^{x \times y} = \log{10}^x + \log{10}^{y} \quad \quad (x > 0,y > 0)

对于涉及指数爆炸的问题，大体有4种处理方法

  • 极力求解 - 知道方法后极力求解。用计算机的性能（超级计算机或并行计算机等）和问题的规模赛跑
    • 缺点：只限于问题规模可控的场景，且效率极低
  • 变相求解 - 转换成简单的问题来求解。比如：利用余数分组等
    • 缺点：并不是所有的指数爆炸问题都能找到比"一个不漏"更好的方法
  • 近似求解 - 不求完全解答，找出相似解。通过估算或使用模拟器等求解方法
    • 缺点：结果可能在数学层面不够严密，但是有助于实际应用
  • 概率求解 - 在实际应用中非常重要，有时能在短时间内解决难题
    • 缺点：需要一点运气。运气不好的话，可能永远找不到答案

不可解问题

反证法

反证法：先假设命题的否定形式成立，然后再进行推理，引出矛盾

因其最后推出荒谬的结果，所以有时也被称为归谬法

思考题：利用反证法证明质数是无穷的

质数：只能被1和本身整除的大于1的整数

2,3,5,7,11,13,17,19,23...

2以外的质数都是奇数，3以外的质数都不是3的倍数，5以外的质数都不是5的倍数...

比n小的质数中，如果存在能够整除n的数，那么n就不是质数

如果n不能被比n小的任何质数整除（即肯定有余数），那么n就是质数

第一步，先假设质数的个数是有限的

所以所有质数的集合可以写为：2,3,5,7,...,P

假设：Q = 2 * 3 * 5 * 7 * ... * P + 1

因为{2,3,5,7,...,P}的个数是有限的，所以Q也是有限的

第二步，引出矛盾

Q比所有的质数{2,3,5,7,...,P}都大，所以Q不是质数

另一方面，Q除以{2,3,5,7,...,P}中的任意一个数都余1（不能整除），所以Q是质数

所以，Q即是质数又不是质数，产生矛盾

所以，质数是无穷的成立

可数

可数：集合的元素是有限的，或者集合中的所有元素都与正整数一一对应

集合的元素是有限的比较容易理解，那集合中的所有元素都与正整数一一对应是什么意思呢？

一、0以上的所有偶数集合是可数的

0,2,4,6,8,10,12...

我们依次为上面集合编号：1,2,3,4,5,6,7...

这里将偶数 2 * (k - 1) 编为 k 号

二、所有整数的集合是可数的

{...-3,-2,-1,0,1,2,3...}

我们可以用编号：1,2,3,4,5,6,7... 分别为：0,1,-1,2,-2,3,-3... 进行编号

重点在于正负交替编号，将所有的正整数编完之后再给负整数编号是行不通的，因为正整数是无穷的

三、所有有理数的集合是可数的

有理数和无理数的区别：有理数可以写成整数、分数、有限小数、无限循环小数，而无理数只能写成无限不循环小数

这样看起来，似乎所有的集合都是可数的，只要集合的所有元素都能与1以上的整数一一对应

但是的确存在一些集合，它是不可数的，我们可以用反证法来进行证明

对角论证法

所有整数数列的集合是不可数的，"无穷个整数的排列"称为"整数数列"

比如：0以上的所有偶数、1以上的所有奇数、斐波那契数列、全0数列、由圆周率的各个数位上的数字组成的整数数列等

我们不可能为实际看到的所有整数数列都编上号，所以我们只需考虑能否"给所有整数数列编号的规律"就行了

然而，无论我们怎么找编号规律，总有遗漏在规律之外的整数数列存在。所以"整数数列的集合是不可数的"

我们先假设所有整数数列的集合是可数的，既然所有整数数列的集合是可数的，那么无论哪个整数数列都可以编号

如上图，1,2,3,4,5,6...k是依次对整数数列进行编号

然后我们按"k+1"的规则做出一个新的整数数列，a1,a2,a3,a4...ak，我们给它命名为ak数列

而这个ak数列不包含在"所有整数数列中"，它与"所有整数数列中"的任一整数数列相比，至少有一处不同

所以"所有整数数列"的集合是不可数的

为了找出不包含在表中的数而选出了表中对角线所在的数字，这种论证法称为对角论证法

不可解问题

所谓不可解问题，并非"花大量时间求解的问题"，也不是"本来就无解的问题"，更不是"目前谁都不知道解法的未解决的问题"

不可解问题是"原则上不能用程序来解决的问题"。也可以说是"不包含在'程序可解决问题的集合'中的问题"

思考题：证明停机问题是不可解问题

停机问题就是判断"某程序在给定数据下，是否会在有限时间内结束运行"的问题

如果能事先判断以下情况编程会方便很多，但是这对人类来说很难做到

  • 该程序会在有限时间内结束运行
  • 该程序永不结束运行

要写出HaltChecker似乎很有难度。HaltChecker必须准确判断给定的程序会如何运行，还可能需要根据给定的数据模拟程序的运行

而且，HaltChecker自身必须要在有限时间内结束运行。即使耗时很长也无妨，关键是必须在有限时间内结束运行并输出判断结果。如果永不结束运行，那么它就不具备作为判断程序的资格

因此，判断程序HaltChecekr，不能通过实际运行对象程序来进行判断。因为如果对象程序永不结束，那么判断程序自身也就永远得不出判断结果

  1. 假设可以写出判断程序HaltChecker。将程序p和数据d输入HaltChecker程序时的结果以函数形式记作：HaltChecker(p, d)

  2. 写出SelfLoop程序，根据HaltChecker，写出如下SelfLoop函数

SelfLoop(p)
{
    halts = HaltChecker(p, p);
    if(halts) {
        while(1 > 0) {

        }
    }
}

SelfLoop会用给定的程序p来判断HaltChecker(p, p)的结果(halfs)，如果结果为true

那么SeltLoop就会陷入无限循环。这里请注意两次输入到HaltChecker中的都是p，即SelfLoop运行如下：

  • 使用HaltChecker，判断"对于程序p，将程序p本身作为数据输入时会不会结束运行"
  • 如果判断结果是会结束运行，那么SelfLoop就会陷入无限循环

  • 如果判断结果是不会结束运行，那么SelfLoop就会马上结束运行

  • 推导出矛盾，将SelfLoop自身传入SelfLoop中。即判断SelfLoop(SelfLoop)的运行情况

SelfLoop(SeltLoop)会在有限时间内结束运行的情况就是HaltChecker(SeltLoop, SelfLoop)为false的情况

而HaltChecker(SelfLoop, SelfLoop)为false的意思是如果将SelfLoop传入SeltLoop，SeltLoop就不会结束运行，这是矛盾的

SeltLoop(SeltLoop)陷入无限循环的情况就是HaltChecker(SeltLoop, SelfLoop)为true的情况

而HaltChecker(SelfLoop, SelfLoop)为true的意思是如果将SelfLoop传入SelfLoop，程序会结束运行，这又是矛盾的

所以，停机问题是不可解问题

如果觉得以上反证法有点绕的话，我们来"感性地讲解"为什么无法写出HaltChecker，若假设HaltChecker是存在的，则可以解决许多尚未解决的问题

费马大定理：当整数n>2时，xn+yn=znx^n + y^n = z^n无整数解

FermatChecker(k)
{
    while(k > 0) {
        // 随意选择几个整数，如：x,y,z,n，其中x,y,z != 0，n > 2
        if(x^n + y^n = z^n) {
            break;
        }
    }
}

哥德巴赫猜想：任一大于3的偶数都可写成两个质数之和

GoldChecker(n)
{
    while(n > 0) {
        if(不能写成2个质数之和) {
            break;
        }
        n = n + 2;
    }
}

总结

在解答问题时，我们要多使用"先用较小的数试算"的方法，用较小的数进行尝试，可以发现规律、性质、结构、循环、一致性等，认清隐含在问题中的模式

如果有"现实世界"解决不了的问题（幻想法则）

  1. 将问题从"现实世界"带到"幻想世界"
  2. 然后在"幻想世界"解决问题
  3. 最后，将答案带回"现实世界"

这个跟高速公路很像，也可以称之为高速公路法则

如果要去很远的地方

  1. 开车上高速公路
  2. 高速开往离目的地较近的出入口
  3. 驶下高速公路，前往目的地

results matching ""

    No results matching ""