离散值的概率分布

期望值、方差、大数定律

  • 对于取值不定的随机值，将其可能的平均取值称为期望值，值的分散情况称为方差
  • 大数定律表明"大量随机值的平均值趋于期望值"，是处理随机数据的基本定理

反复抛掷硬币，首次正面朝上与抛掷硬币次数一致的概率

抛N次硬币的结果如下：

正、反正、反反正、反反反正、反反反反正、...、反×t正

1/2、1/4、1/8、1/16、1/32、....、1/2t 1/2^t

P(X=t)=1/2t(t=1,2,3,...) P(X=t) = 1/2^t \quad\quad(t=1,2,3,...)

1/2 + 1/4 + 1/8 + 1/16 + 1/32 + ... = 1

我们可以通过等比数列公式计算该值，(首项-末项的后项)/(1-公比)

1/2 + 1/4 + ... + 1/2t 1/2^t = 1/2−(1/2)t+11−1/2=(1/2)(1−(1/2)t)1/2=1−12t \frac{1/2 - (1/2)^{t+1}}{1-1/2} = \frac{(1/2)(1-(1/2)^t)}{1/2} = 1 - \frac{1}{2^t}

因为 t -> ∞，所以极限收敛于1

离散值的概率一览

如果设定问题时明确假定了结果独立，我们就不必再专门申明。不过在书写正式的报告或论文时最好还是不要省略，全部明确写明为好

于是，通常情况下，离散值的概率一览只需满足以下条件即可

  • 每一条概率都大于等于0
  • 所有概率之和为1

二项分布

特殊的概率分布通常会以专门的名称表示。其中，二项分布是一种基本的类型

二项分布表示"硬币正面向上的概率为p时，掷硬币n次后正面向上的次数"

也就是说，假设概率p为1，且有出现0的概率为q=(1-p)的独立随机变量Z1,Z2,...Zn，X=Z1+Z2+...+Zn的分布就是一种二项分布

二项分布的具体形状由n与p决定。因此，二项分布（binomial distribution）也能记为Bn(n,p)

图3.2列举了几种不同的二项分布

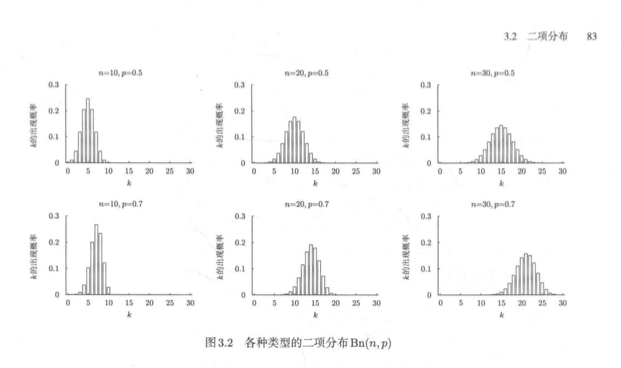
二项分布具体例子

假设硬币正面向上的概率为p，试求抛掷n=7次后正面向上3次的概率P(X=3)

下面列出了所有X=3的Z1到Z7的可能情况。○表示正面向上，●表示反面向上，共计35种组合

接下来，我们只需分别求出各种情况的概率即可

模式"●●●●○○○"的概率为qqqqppp=p3q4 p^3q^4

模式"●●●○●○○"的概率为qqqpqpp=p3q4 p^3q^4

模式"●●●○○●○"的概率为qqqppqp=p3q4 p^3q^4

...

显然，每一种情况都是3个○与4个●而3个p与4个q相乘后得到的结果始终为p3q4 p^3q^4

又由于共有35种情况，我们将得到以下结果

P(X=3) = 35p3q4 35p^3q^4

现在我们将该问题推而广之，求在任意n、p与k的条件下P(X=k)的值

不难看出，符合X=k的模式Z1,Z2,...,Zn的模式共有Cnk C_n^k 种

这些模式的概率分别为pkqn−k p^kq^{n-k} ，因此我们能得到如下答案

P(X=k)=Cnkpkqn−k(k=0,1,2,...,n) P(X=k) = C_n^kp^kq^{n-k} \quad\quad (k=0,1,2,...,n)

又因为，p = 1 - q，所以

P(X=k)=Cnkpk(1−p)n−k(k=0,1,2,...,n) P(X=k) = C_n^kp^k(1-p)^{n-k} \quad\quad (k=0,1,2,...,n)

期望值

概率理论通过随机变量来表现不确定的随机值。我们可以使用学过的技巧来计算概率分布

对于我们关注的值X，它有○○的概率取这个值，有△△的概率取那个值

不过，在求X时，我们需要首先知道相关的A、B、C等值的概率分布

然而，这种以概率分布的形式求取结果的方法并不那么容易理解，尤其是在我们需要考虑X、Y、Z等多个值的时候，很难把握各种概率分布之间的关系，也不便进行比较

此时，如果我们可以得出不含随机性的具体数值，即尽管单次结果随机确定，但平均值恒定，就能更深入地讨论问题，这就是期望值

在将概率理论应用至某类具体的现实问题时，我们常会根据需要定义X，并尽可能使X的期望值最大。在分析这类问题时会大量使用期望值，因此我们必须掌握期望值的性质

期望值的定义

假设：P(X=1) = 1/2，P(X=2) = 1/3，P(X=5) = 1/6

我们以上帝视角将每个世界ω所对应的X(ω)作为高度绘图（画立体图），如下：

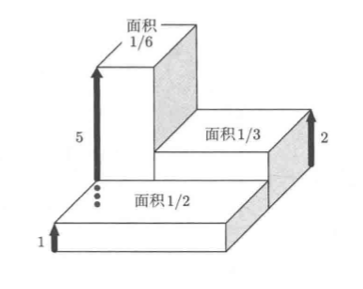
这一块状体的体积称为期望值(expectation)，记为E[X]。我们可以通过下面的算式分别计算各个块状体的体积并求和，得到具体的期望值

E[X] = (高1) * (底面积1/2) + (高2) * (底面积1/3) + (高3) * (底面积1/6) = 1 * P(X=1) + 2 * P(X=2) + 5 * P(X=5) = 2

我们可以将期望值理解为所有平行世界的平均值，下面这个雪国的故事可以帮助我们理解这个概念

假设。Ω国有A、B、C三个省，各省的面积分别为1/6、1/3与1/2，全国各总面积为1/6+1/3+1/2=1

某一天，Ω国下雪了。A省、B省和C省的积雪分别是5m、2m与1m。每个省的积雪情况不同，那么全国的平均积雪状况如何呢

也就是说，如果将积雪平整地铺满整个国家，积雪将有多深呢？答案是E[X]

这是因为，如前所述，计算出的体积除以全国的总面积后得到的结果，正是积雪平铺的高度(平均积雪)

由于全国的总面积为1，因此该体积的值就等于平均积雪

如果X为负，就表示该区域处于低洼处。在计算期望值时，必须用其他区域的降雪填满这些低洼处

如果无法填满所有的低洼处，期望值就将为负

期望值的基本性质

E[X] = ∑kkP(X=k) \displaystyle\sum_{k}kP(X=k)

E[g(X)] = ∑kg(k)P(X=k) \displaystyle\sum_{k}g(k)P(X=k) \quad\quad (g表示某种函数)

如果要求○○的期望值，只需分别计算各种情况下"○○的值与该情况发生概率的乘积"，并将它们相加即可

期望值练习题

在按下按钮后，自动赌博机会显示相应图案并吐出硬币，硬币个数Y遵从下面的概率分布。试求Y的期望值

  • P(Y=0) = 0.7
  • P(Y=2) = 0.29
  • P(Y=30) = 0.01

E[Y] = 0 * 0.7 + 2 * 0.29 + 30 * 0.01 = 0.88

随机变量X值为1的概率为1/2，值为2的概率为1/3，值为5的概率为1/6，试求E[(X−3)2]E[(X-3)^2]

E[(X−3)2]=(X−3)2∗1/2+(X−3)2∗1/3+(X−3)2∗1/6E[(X-3)^2] = (X-3)^2 * 1/2 + (X-3)^2 * 1/3 + (X-3)^2 * 1/6 = 4 * 1/2 + 1 * 1/3 + 4 * 1/6 = 3

期望值还有一个性质，即当X始终大于某个常量c时，则E[X]>c（任一随机值都大于c，则平均值肯定大于c）

E[X + c] = E[X] + c（所有随机值都加c，则平均值也加c）

E[cX]= cE[X]（所有随机值都乘c，则平均值也乘c）

类似地，对于随机变量X与Y，和的期望值等于期望值之和

E[X+Y]= E[X]+E[Y]（所有随机值相加求平均，和分别求平均再相加，结果相等）

二项分布Bn(n,p)的期望值

直接通过 P(X=k)=Cnkpk(1−p)n−k(k=0,1,2,...,n) P(X=k) = C_n^kp^k(1-p)^{n-k} (k=0,1,2,...,n) 与 ∑kkP(X=k) \displaystyle\sum_{k}kP(X=k) 计算它的期望值有时并不容易

不过，如果我们"假设有独立的随机变量Z1,Z2,...,Zn，它们取值1的概率为p，取值0的概率为(1-p)，期望值X是所有这些随机变量之和"

E[X] = E[Z1+Z2+...+Zn] = E[Z1] + E[Z2] + ... + E[Zn] = p + p + ... + p = np

期望值乘法运算的注意事项

在计算随机变量X与Y的期望值相乘之积E[XY]时，我们必须注意独立性的问题。X与Y独立与否将对结果产生影响

设去年的积雪量为X，且今年的积雪量是去年的Y倍

即，去年Ω上的各点ω覆盖了X(ω)的雪，今年则增加至了去年的Y(ω)倍。于是，今年的积雪能够以Z=XY表示

现在，我们设全国有一半的土地Y=2，另一半Y=1，于是E[Y] = 2 * 1/2 + 1 * 1/2 = 1.5

此时，E[Z]=E[XY]=1.5E[X]是否成立？

如果X与Y独立，上面的等式的确成立。如果两者独立，即使X的值已限定（也可以取任意合适的值），都不受Y的限制

例如，当X=5时，我们依然能确保一半的土地Y=2，另一半Y=1。因此，在X=5的区域中，有一半Y=2，另一半Y=1，该部分的体积变为原来的1.5倍

其他部分也都如此，最终整体的体积也变为原来的1.5倍

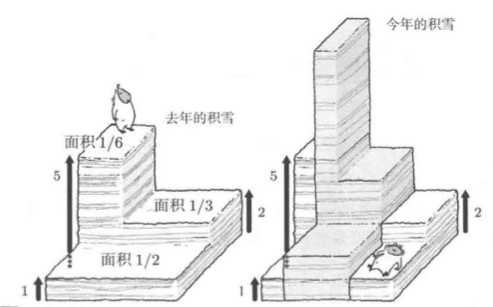
然而，如果随机变量并不独立，E[Z]就不一定等于1.5E[X]。根据积雪量倍增的具体区域的不同，今年降雪的总体积也将发生变化

期望值乘法运算练习题

随机变量X与Y的联合分布如下表所示，试求两者之积XY的期望值E[XY]，并与E[X]E[Y]比较

X = 1 X = 2 X = 4
Y = 1 2/8 2/8 1/8
Y = 2 1/8 1/8 1/8

E[XY] = [(各种情况下XY的值) * (该情况发生的概率)]之和

= (1 * 1) * P(X=1,Y=1) + (2 * 1) * P(X=2,Y=1) + (4 * 1) * P(X=4,Y=1) + (1 * 2) * P(X=1,Y=2) + (2 * 2) * P(X=2,Y=2) + (4 * 2) * P(X=4,Y=2)

= 1 * 2/8 + 2 * 2/8 + 4 * 1/8 + 2 * 1/8 + 4 * 1/8 + 8 * 1/8 = 24/8 = 3

E[X] = 1 * (2/8+1/8) + 2 * (2/8+1/8) + 4 * (1/8+1/8) = 17/8

E[Y] = 1 * (2/8+1/8+1/8) + 2 * (1/8+1/8+1/8) = 11/8

所以，E[XY] ≠ E[X]E[Y]（3 ≠ 187/64）

期望值不存在的情况

上面讨论的都是可取的值有限的情况，我们只需通过步骤固定的计算就能得到期望值。如果随机变量可取任意的整数值，期望值就不一定存在

期望值存在的例子：例如："反复抛掷硬币，首次正面朝上与抛掷硬币次数一致的概率"

E[X]=1∗1/2+2∗1/4+3∗1/8+...+n∗1/n2=2 E[X]= 1 * 1/2 + 2 * 1/4 + 3 * 1/8 + ... + n * 1/n^2 = 2

期望值不存在的例子(1)--发散至无穷大

接下来是一个期望值不存在的例子(级数发散)。与之前一样，我们将不断抛掷硬币，直至得到正面向上的结果

  • 如果第1次就得到正面向上的结果(X=1)，奖金为2元
  • 如果第1次就得到正面向上的结果(X=2)，奖金为4元
  • 如果第1次就得到正面向上的结果(X=3)，奖金为8元
  • ...

试求获得的奖金Y=2X的期望值E[Y]，我们可以据此列出以下式子

E[Y]=2∗1/2+4∗1/4+8∗1/8+...+2n∗1/2n=1+1+1+...+1 E[Y]= 2 * 1/2 + 4 * 1/4 + 8 * 1/8 + ... + 2^n * 1/2^n = 1 + 1 + 1 + ... + 1

所以，E[Y] = ∞

期望值不存在的例子(2)--由无穷大减无穷大得到的待定型

我们再来看一个情况更加复杂的例子。对于之前的X，如果Z=(−2)XZ=(-2)^X，期望值又会如何呢?

E[Z]=(−2)1+(−2)2+(−2)3+...+(−2)X=−2+4+(−8)+...+(−2)X E[Z]= (-2)^1 + (-2)^2 + (-2)^3 + ... + (-2)^X = -2 + 4 + (-8) + ... + (-2)^X

整理正数和负数可得，E[Y] = ∞ - ∞

我们来总结一下以上分析结果（使用雪国的例子）。通常，对于随机变量R来说，以下结论成立

  • 积雪与低洼处的体积都有穷→期望值存在(E[R]是有穷值)
  • 积雪的体积无穷，低洼处的体积有穷→期望值不存在(E[R]=∞)
  • 积雪的体积有穷，低洼处的体积无穷→期望值不存在(E[R]=-∞)
  • 积雪与低洼处的体积都无穷→期望值不存在(E[R]是待定型)

有些书将期望值解释为重心，比如：胖子和瘦子玩跷跷板，那么胖子需要在杠杆的更里侧而瘦子需要在杠杆的更外侧

最终杠杆平衡的点就是期望值，跟雪国的例子大同小异，这里不再赘述

方差与标准差

尽管期望值是分布的首要描述指标，但仅凭它还无法判断数值的离散情况。为此，我们希望找到另一种指标，补充期望值的这一不足。这就是下文将要讲的方差

方差即"期望值离散程度"的期望值

设随机变量X的期望值E[X]=μ。习惯上，随机值X以大写字母表示，它的期望值μ是一个定值，因此用小写字母表示

由于X是一个随机变量，因此即使它的期望值为μ，也不表示它的值就一定等于μ。为此，我们需要计算它的实际取值x与μ的差距

测量(或者说定义这种偏差)的方式有很多，|x-μ|可能是最为直观的方法，但落实到具体计算时，绝对值的存在会带来诸多不便(有时问题不得不分情况讨论，或是由于对应的曲线包含折角而无法微分等)

于是，通常使用偏差的平方(x−μ)2 (x - \mu)^2 而非绝对值来解决实际问题

  • 如果X的取值正巧为μ，(x−μ)2=0(x-\mu)^2=0
  • 否则(x−μ)2>0(x-\mu)^2>0
  • 且x与μ的偏差越大，(x−μ)2(x-\mu)^2的值也越大

在确定了标准之后，我们就可以以此测量具体的离散程度。不过由于X是一个随机值，直接计算(X−μ)2(X-\mu)^2得到的也将是一个随机值

而我们希望得到的是一种数值固定的指标，因此需要进一步计算它的期望值E[(X−μ)2]E[(X-\mu)^2]来消除其中的随机性

用这种方式得到的"离散程度的期望值"称为方差(variance)，记为V[X]或Var[X]

V[X]=E[(X−μ)2]V[X]=E[(X-\mu)^2]，其中μ=E[X]，X是随机值，V[X]和E[X]是固定值。V[X]>=0

只要知道随机变量X的期望值E[X]与方差V[X]，我们就能判断X的取值的大致范围，以及它与某个值的离散程度

尤其当V[X]=0时，就表示该变量完全不含随机成分。这是因为当E[(X−μ)2]=0E[(X-\mu)^2]=0时P(X=μ)必然为1。X不等于μ的概率为零

此外，根据定义，我们能很容易看出在E[X]=0时E[X2]=V[X]E[X^2]=V[X]的事实。有时，这个性质对解决问题很有帮助

标准差

我们已经在为随机变量X引入主要指标期望值E[X]后，又进一步引入了次要指标方差V[X]，以度量随机变量的离散程度

之前说过方差通常使用偏差的平方，而标准差就是把这个平方再开根号即可

标准差(standard deviation)，通常记为σ或s。σ=V[X]\sigma=\sqrt{V[X]}

在统计学相关图书中"记方差为σ2\sigma^2"的表述十分常见，于是标准差的记法也沿用了这一习惯

常量的加法、乘法及标准化

接下来，我们来了解下方差与标准差的性质。与期望值一样，我们首先来看一下它们的计算

Y = X + c，Z = cX（X、Y、Z是随机变量，c是常量）

方差如下：

  • V[Y]=V[X+c]=V[X]（增加常量c后，方差不变）
  • V[Z]=V[cX]=c2V[X]V[Z]=V[cX]=c^2V[X]乘以常量c后，方差将变为原来的c2c^2倍

换言之，它们的标准差有以下性质：

  • 在加上常量 c之后，标准差不变
  • 在乘上常量c之后，标准差扩大至原来的|c|倍

概率分布图如下：

推导如下：

设E[X]=μ，我们将得到E[Y]=μ+c与E[Z]=cμ

V[Y]=E[(Y−(μ+c))2]=E[((X+c)−(μ+c))2]=E[(X−μ)2]=V[X]V[Y]=E[(Y-(\mu+c))^2]=E[((X+c)-(\mu+c))^2]=E[(X-\mu)^2]=V[X]

V[Z]=E[(Z−cμ)2]=E[(cX−cμ)2]=E[c2(X−μ)2]=c2E[(X−μ)2]=c2V[X]V[Z]=E[(Z-c\mu)^2]=E[(cX-c\mu)^2]=E[c^2(X-\mu)^2]=c^2E[(X-\mu)^2]=c^2V[X]

根据上述性质，我们能够通过转换随机变量X来获得需要的期望值与方差。现设E[X]=μ，V[X]=σ2>0V[X]=\sigma^2>0

此时，只要令W=X−μσW=\frac{X-\mu}{\sigma}，就能得到E[W]=0且V[W]=1

E[W]=E[X−μσ]=E[X−μ]σ=E[X]−μσ=μ−μσ=0 E[W] = E[ \frac{X-\mu}{\sigma} ] = \frac{ E[X - \mu] }{\sigma} = \frac{ E[X] - \mu }{\sigma} = \frac{ \mu - \mu }{\sigma} = 0

V[W]=V[X−μσ]=V[X−μ]σ2=V[X]σ2=σ2σ2=1 V[W] = V[ \frac{X-\mu}{\sigma} ] = \frac{ V[X - \mu] }{\sigma^2} = \frac{ V[X]}{\sigma^2} = \frac{ \sigma^2 }{\sigma^2} = 1

这种将期望值化为0，方差化为1的转换处理称为标准化(或称归一化)，第4、5、8章节会进一步讨论

作为惯例，在对收集到的不同类型的数据进行正式处理前，我们通常需要对它们分别做标准化处理

例如，我们会在比较难易度不同的考试的成绩时引入偏差值，这本质上也是一种标准化

各项独立时，和的方差等于方差的和

如果X与Y独立，则V[X+Y]=V[X]+V[Y]成立

设E[X]=μ E[X] = \mu ，E[Y]=ν E[Y] = \nu

V[X+Y]=E[((X+Y)−(μ+ν))2] V[X+Y]=E[((X+Y)-(\mu+\nu))^2] =E[((X−μ)+(Y−ν))2]=E[((X-\mu)+(Y-\nu))^2] =E[(X−μ)2+(Y−ν)2+2(X−μ)(Y−ν)]=E[(X-\mu)^2+(Y-\nu)^2+2(X-\mu)(Y-\nu)] =E[(X−μ)2]+E[(Y−ν)2]+E[2(X−μ)(Y−ν)]=E[(X-\mu)^2]+E[(Y-\nu)^2]+E[2(X-\mu)(Y-\nu)] =V[X]+V[Y]+2E[(X−μ)(Y−ν)]=V[X]+V[Y]+2E[(X-\mu)(Y-\nu)]

由于X与Y独立，因此X-μ与Y-ν也独立。又由于递等式最后一行的后半部分值为0，因此V[X+Y]=V[X]+V[Y]成立

2E[(X - μ)(Y - ν)] = 2E[X - μ]E[Y - ν] = 2(μ - μ)(ν - ν) = 0

对于多个随机变量的情况，结论依然相同。例如，如果X、Y与Z独立，则V[X+Y+Z] = V[X]+V[Y]+V[Z]成立

试求二项分布Bn(n,p)的方差

假设我们有独立的随机变量Z1,Z2,...,Zn，它们取值为1的概率为p，取值为0的概率q=1-p

这些随机变量之和X=Z1+Z2+...+Zn，并遵从二项分布Bn(n,p)。我们可以根据独立性得到它的方差

V[X] = V[Z1] + V[Z2] + ... + V[Zn]

且根据定义，我们可以像下面这样计算个别的方差

V[Zt]=E[(Zt−p)2]=(1−p)2p+(0−p)2q=q2p+p2q=pq(q+p)=pq(t=1,...,n) V[Z_t] = E[(Z_t-p)^2] = (1-p)^2p + (0-p)^2q = q^2p + p^2q = pq(q+p) = pq\quad(t=1,...,n)

综上，Bn(n,p)的方差V[X] = npq = np(1-q)

平方的期望值与方差

随机变量X的方差 = X的平方的期望值 - X的期望值的平方

V[X]=E[X2]−E[X]2 V[X] = E[X^2] - {E[X]}^2

这条公式也可以改写成

σ2=E[X2]−μ2 \sigma^2 = E[X^2] - \mu^2 -> E[X2]=μ2+σ2 E[X^2] = \mu^2 + \sigma^2

也就是说，X的平方的期望值等于X的期望值的平方加上X的方差

该公式成立的理由如下。设Z=X-μ，则有E[Z]=0，且X=Z+μ

于是，随机变量X就被分为了期望值μ与对应的随机变量Z。我们可以借助随机变量Z展开下式

E[X2]=E[(Z+μ)2]=E[Z2+μ2+2μZ]=E[Z2]+E[μ2]+E[2μZ] E[X^2] = E[(Z+\mu)^2] = E[Z^2 + \mu^2 + 2\mu Z] = E[Z^2] + E[\mu^2] + E[2\mu Z]

=E[Z2]+μ2+2μE[Z]=V[X]+μ2 = E[Z^2] + \mu^2 + 2\mu E[Z] = V[X] + \mu^2

其中，由于Z=X-μ且E[Z]=0，因此有E[Z2]=V[X]E[Z^2]=V[X]且2μE[Z]=0

平方的期望值与方差练习题

一、随机变量X取值-1的概率为1/3，取值+1的概率为2/3，试求该随机变量的方差（使用上述公式）

无论X=-1或X=1，X2=1X^2=1，所以E[X2]=1E[X^2]=1，而E[X] = -1 * 1/3 + 1 * 2/3 = 1/3

所以，V[X]=1−(13)2=89 V[X] = 1 - (\frac{1}{3})^2 = \frac{8}{9}

二、当E[X]=μ且V[X]=σ2 V[X]=\sigma^2 时，试证明对于取值恒定的常量a,以下等式成立

E[(X−a)2]=(μ2−a)2+σ2 E[(X-a)^2] = ( \mu^2 - a)^2 + \sigma^2

设 Y = X - a，则有

E[(X−a)2]=E[Y2]=E[Y]2+V[Y]=E[X−a]2+V[X−a] E[(X-a)^2] = E[Y^2] = E[Y]^2 + V[Y] = E[X-a]^2 + V[X-a]

=(E[X]−a)2+V[X]=(μ−a)2+σ2 = (E[X] - a)^2 + V[X] = (\mu - a)^2 + \sigma^2

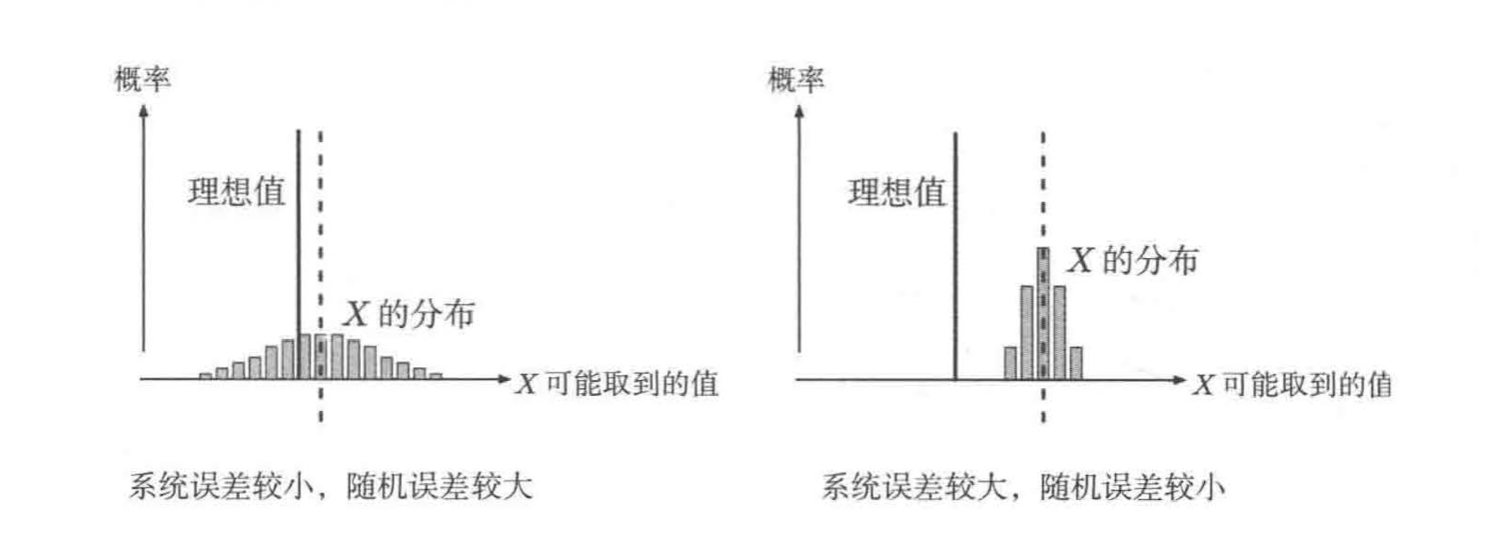
系统误差与机会误差

(X与a的平方误差的期望值) = (期望值的平方误差) + 方差 = (由偏移引起的误差) + (由离散引起的误差)

如果要通过概率手段对数据进行处理，就必须小心处理系统误差(又称偏性误差，表现为数值整体偏移)与随机误差(又称机会误差，表现为数值离散)

生产工艺A的质检结果如左图所示，看似误差较小，其实数值较为离散。右图表示的生产工艺B，虽然误差较大，反而更加优秀

其他

样本方差的无偏估计（分母-1）会在后续章节讨论

正态分布的情况下，随机变量的取值99.7%都在正负3倍的标准差范围内

标准化这个词可能会存在一些差异，与其说标准化是一个专有名词，不如说它是一个普通名词。只要是需要依照某种标准对对象进行处理，我们都可以称其为标准化

大数定律

随机变量的数量越多，它们的平均值就越趋于稳定，在分析处理随机变量时，这是一条非常重要的性质

独立同分布

独立同分布的英语是independent and identically distributed，可省略为i.i.d.

  • 每一个随机变量对应的分布（边缘分布）都相同
  • 任意随机变量都相互独立

比如：投掷骰子20次，结果为1、2、3、4、5、6的概率分别为1/6，但每次投掷的结果都是独立的

假设骰子被做了手脚，但是中间过程没有人为干预。比如：1、2、3、4、5、6的概率分布分别为：0.4、0.1、0.1、0.1、0.1、0.2

那么投掷20次后，点数为1的概率还是接近0.4，这种情况"做手脚的骰子"也是遵从i.i.d.的

平均值的期望值与平均值的方差

虽然在很多情况下，平均值和期望值经常会混用，但是它们是有区别的

对于随机变量X1,X2,X3,...,Xn，它们的平均值（总和/数量）仍然是一个随机值

  • 恒定值的平均值仍然是恒定值
  • 随机值的平均值仍然是随机值

期望值是通过横向计算不同平行世界而求得的恒定值。对于本例中的随机变量Z，它的期望值是各个期望值的平均

E[Z]=E[X1+X2+...+Xnn]=E[X1+X2+...+Xn]n=E[X1]+E[X2]+...+E[Xn]n E[Z] = E[ \frac{X_1 + X_2 + ... + X_n}{n}] = \frac{E[X_1 + X_2 + ... + X_n]}{n} = \frac{E[X_1] + E[X_2] + ... + E[X_n]}{n}

又由于X1,X2,X3,...,Xn遵从i.i.d.，因此它们自然都与期望值(设为μ)相同。于是，我们可以得到随机变量Z的期望值

E[Z]=nμn=μ E[Z] = \frac{n\mu}{n} = \mu

Z的期望值与每个单独的期望值一致，这也符合我们预期的结果，接下来我们再计算一下Z的方差

V[Z]=V[X1+X2+...+Xnn]=V[X1+X2+...+Xn]n2 V[Z] = V[ \frac{X_1 + X_2 + ... + X_n}{n}] = \frac{V[X_1 + X_2 + ... + X_n]}{n^2}

此时，如果X1,X2,X3,...,Xn独立，则如下关系成立

V[Z]=V[X1]+V[X2]+...+V[Xn]n2 V[Z] = \frac{V[X_1] + V[X_2] + ... + V[X_n]}{n^2}

进一步讲，当X1,X2,X3,...,Xn遵从i.i.d.，则方差显然相同，于是得到如下结果

V[Z]=nσ2n2=σ2n V[Z] = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n}

如果实验或调查的设计非常理想，每个事件的条件相同且相互独立，那么在求n次结果的平均值时，方差必然为1/n。这是处理随机值的一条基本常识

方差为1/n，就意味着标准差为1/n 1 / \sqrt{n} 。如果希望将精度增加10倍（即把结果与期望值之间的平均误差缩小至原本的1/10），测试次数就必须增加102=10010^2=100倍。仅增加10倍测试量无法提升10倍的精度

大数定律总结

随机变量的期望值与原来相同，方差是原来的1/n（标准差1/n 1 / \sqrt{n} ）

如果n可以无限增大，那么方差则可以无限减小并趋近于0

方差为零表示不含随机性。简单来讲，如果随机变量的个数n无限增加，它们的平均值将逐渐收敛于μ。这就是所谓的大数定律

大数定律相关注意事项

  • 只有在随机变量之和除以n后，大数定律才成立。如果只是单纯求和，方差将不断增大
  • 如果是期望值不存在的概率分布，大数定律将不再成立
  • 本书已经讨论了方差存在且随机变量遵从i.i.d.的情况。事实上，我们可以进一步放宽这一前提条件

条件期望

如果我们知道X=a这一观测值，只要进一步计算条件期望P(Y=b|X=a)，就能估计出Y的值

通过计算条件期望，我们可以对随机变量的取值概率做出预估。不过，我们有时并不满足于仅得出一些可能的情况，而是希望得到更精确的估计值

此时，我们首先想到的自然是选择条件概率P(Y=b|X=a)的值最大的b作为答案。如果需要尽可能提高估计的精度，这种做法很符合常理

另一种做法是求在X=a时Y的条件分布(即各个值的出现概率)，并计算相应的期望值（条件期望）

E[Y∣X=a]=∑bbP[Y=b∣X=a] E[Y|X=a] = \displaystyle\sum_{b}bP[Y=b|X=a]

对于取值不同的X，条件期望E[Y|X=a]的值也不同。如果可以知道X各种取值的出现概率，条件期望最终的计算结果将与通常的期望值一致

E[Y]=∑aE[Y∣X=a]P(X=a) E[Y] = \displaystyle\sum_{a}E[Y|X=a]P(X=a)

最小二乘法

假设有条件分布P(Y=b|X=a)。试编写一个程序，使它能在输入X之后输出Y的估计值Y^\hat Y，并使平方误差(Y−Y^)2 (Y- \hat Y)^2 的期望值E[(Y−Y^)2] E[(Y- \hat Y)^2] 尽可能小

换言之，我们要求的是所有在输入X后输出Y的估计值的函数中，E[(Y−g(X))2] E[(Y- g(X))^2] 的值最小的那个。这个问题的答案正是条件期望：g(a) = E[Y|X=a]

上述等式成立的理由如下。为简化问题，我们具体设X可以取值1、2、3。误差的期望值如下：

E[(Y−Y^)2]=E[(Y−g(X))2] E[(Y- \hat Y)^2] = E[(Y- g(X))^2]

=∑a=13∑b(b−g(a))2P(X=a,Y=b) = \displaystyle\sum_{a=1}^3 \displaystyle\sum_{b} (b-g(a))^2P(X=a,Y=b)

=∑b(b−g(1))2P(X=1,Y=b) = \displaystyle\sum_{b} (b-g(1))^2P(X=1,Y=b)

+∑b(b−g(2))2P(X=2,Y=b) + \displaystyle\sum_{b} (b-g(2))^2P(X=2,Y=b)

+∑b(b−g(3))2P(X=3,Y=b) + \displaystyle\sum_{b} (b-g(3))^2P(X=3,Y=b)

=(取决于g(1)的量)+(取决于g(2)的量)+(取决于g(3)的量)

该期望值可以分为3部分。因此，我们只要分别求出各部分的解，就能得到最佳的g，如下所示：

  • 定义g(1)，使∑b(b−g(1))2P(X=1,Y=b) \displaystyle\sum_{b} (b-g(1))^2P(X=1,Y=b)能有最小值
  • 定义g(2)，使∑b(b−g(2))2P(X=2,Y=b) \displaystyle\sum_{b} (b-g(2))^2P(X=2,Y=b)能有最小值
  • 定义g(3)，使∑b(b−g(3))2P(X=3,Y=b) \displaystyle\sum_{b} (b-g(3))^2P(X=3,Y=b)能有最小值

那么，试着根据该方针来定义g(1)吧。为便于阅读，我们用g1g_1表示g(1)，于是可以得到以下等价形式

∑b(b−g1)2P(X=1,Y=b) \displaystyle\sum_{b} (b-g_1)^2P(X=1,Y=b)

=∑b(b−g1)2P(Y=b∣X=1)P(X=1) = \displaystyle\sum_{b} (b-g_1)^2P(Y=b|X=1)P(X=1)

=P(X=1)∑b(b−g1)2P(Y=b∣X=1) = P(X=1) \displaystyle\sum_{b} (b-g_1)^2P(Y=b|X=1)

要求它的最小值，其实就是求∑b(b−g1)2P(Y=b∣X=1) \displaystyle\sum_{b} (b-g_1)^2P(Y=b|X=1)的最小值， 为此，我们先定义h1h_1

h1(g1)=∑b(b−g1)2P(Y=b∣X=1) h_1(g_1) = \displaystyle\sum_{b} (b-g_1)^2P(Y=b|X=1)

再计算它的微分

dh1dg1=2∑b(g1−b)P(Y=b∣X=1) \frac{dh_1}{dg_1} = 2\displaystyle\sum_{b}(g_1-b)P(Y=b|X=1)

=2(∑bg1P(Y=b∣X=1)−∑bbP(Y=b∣X=1)) = 2(\displaystyle\sum_{b}g_1P(Y=b|X=1) - \displaystyle\sum_{b}bP(Y=b|X=1))

=2(g1∑bP(Y=b∣X=1)−∑bbP(Y=b∣X=1)) = 2(g_1\displaystyle\sum_{b}P(Y=b|X=1) - \displaystyle\sum_{b}bP(Y=b|X=1))

=2(g1−E[Y∣X=1]) = 2(g_1 - E[Y|X=1])

由此可知，当dh1/dg1=0dh_1 / dg_1 = 0时，即g1=E[Y∣X=1]g_1=E[Y|X=1]时，h1(g1)h_1(g_1)能取到最小值

注释：当g1<E[Y∣X=1] g_1 < E[Y|X=1] 时 dh1/dg1<0dh_1 / dg_1 < 0，当g1>E[Y∣X=1] g_1 > E[Y|X=1] 时 dh1/dg1>0dh_1 / dg_1 > 0，所以在 g1=E[Y∣X=1] g_1=E[Y|X=1] 时最小

另外还需要注意：h1(g1)=E[(Y−g1)2∣X=1]h_1(g_1) = E[(Y-g_1)^2|X=1]

h2(g2)h_2(g_2) 、h3(g3) h_3(g_3) 同理，因此能推出g(a)=E[Y|X=a]的结论

我们通过上帝视角再来看一下g(a)

我们先把g(a)理解为一个普通的函数，输入具体数值a，返回一个确定值g(a)

如果给g提供一个随机值X，就能得到一个与X对应的随机值 Y^=g(X) \hat Y = g(X)

此处的g(X)可以记为E[Y|X]（不要记作：E[Y|X=X]，这样的话就变成E[Y]了）

光看数学表达式可能不易理解，我们用上帝视角了解它的明确含义。简单来讲，该函数的作用是整平了X相同的区域

条件方差

设 E[Y|X=a] = μ(a)，我们可以据此求得相应的条件方差

V[Y∣X=a]=E[(Y−μ(a))2∣X=a] V[Y|X=a] = E[(Y-\mu(a))^2|X=a]

只要将方差的定义中出现的所有期望值替换为条件期望即可

需要注意的是，∑aV[Y∣X=a]P(X=a) \displaystyle\sum_{a} V[Y|X=a]P(X=a)通常与V[Y]不等

举一个极端的例子，尽管当X=Y时，V[Y|X=a] = V[a|X=a] = 0 始终成立，但这并不意味着V[Y]就一定等于0

投资建议

假设给你100块去赌场，有2个套餐给你选择，你会选择哪一个呢

  • 1个赌桌，胜率90%，赢了翻倍，输了归零。离开赌桌的条件是参与100次或金额归0
  • 10个赌桌，其中6个胜率60%，另外4个胜率40%，同样赢了翻倍，输了归0。但是你每次都会将金额平均分成10份，分别参与10个赌桌（视为一次）。离开赌桌的条件同样也是参与100次或金额归0
class Test
{
    public function run()
    {
        for ($j = 0; $j < 10; $j++) {
            $money = 100;
            for ($i = 0; $i < 100; $i++) {
                $money = $this->balance($money, 0.9);
            }
            $this->line("一个篮子：{$money}");
        }

        for ($j = 0; $j < 10; $j++) {
            $money = 100;
            for ($i = 0; $i < 100; $i++) {
                $money1 = $this->balance($money * 0.1, 0.6);
                $money2 = $this->balance($money * 0.1, 0.6);
                $money3 = $this->balance($money * 0.1, 0.6);
                $money4 = $this->balance($money * 0.1, 0.6);
                $money5 = $this->balance($money * 0.1, 0.6);
                $money6 = $this->balance($money * 0.1, 0.6);
                $money7 = $this->balance($money * 0.1, 0.4);
                $money8 = $this->balance($money * 0.1, 0.4);
                $money9 = $this->balance($money * 0.1, 0.4);
                $money10 = $this->balance($money * 0.1, 0.4);
                $money = $money1 + $money2 + $money3 + $money4 + $money5 + $money6 + $money7 + $money8 + $money9 + $money10;
            }
            $this->line("十个篮子：{$money}");
        }
    }

    protected function balance($money, $percent)
    {
        if (mt_rand(1, 10) > $percent * 10) {
            $money = 0;
        } else {
            $money = $money * 2;
        }
        return $money;
    }
}

(new Test())->run();

results matching ""

    No results matching ""