模型优化

模型有了损失函数，才能够进行学习。那么问题来了，模型是如何通过损失函数进行学习的呢？

我们还需要了解：前馈网络、导数与链式法则、反向传播、优化方法等。当我们掌握这些内容后，我们就可以将模型学习的过程串起来作为一个整体，彻底搞清楚怎样通过损失函数训练模型

前馈网络

前馈网络，也称为前馈神经网络。顾名思义，是一种“往前走”的神经网络。它是最简单的神经网络，其典型特征是一个单向的多层结构。简化的结构如下图：

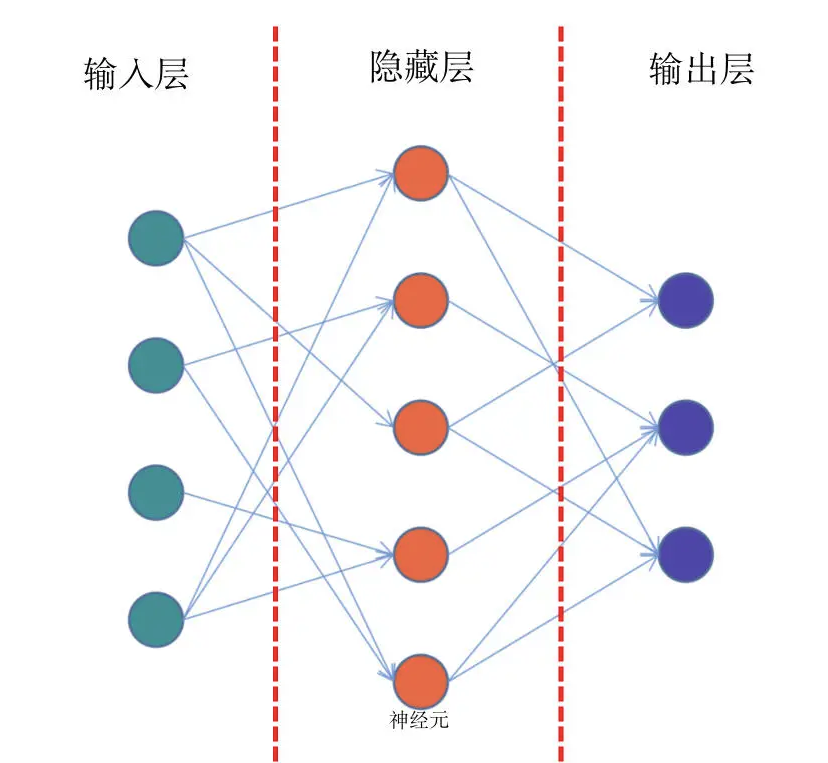
结合上面的示意图，我们看到最左侧的绿色的一个个神经元，它们相当于第0层，一般适用于接收输入数据的层，所以我们把它们叫做输入层

比如我们要训练一个y=f(x)函数的神经网络，x作为一个向量，就需要通过这个绿色的输入层进入模型。那么在这个网络中，输入层有5个神经元，这意味着它可以接收一个5维长度的向量

结合图解，我们继续往下看，网络的中间有一层红色的神经元，它们相当于模型的“内部”，一般来说对外不可见，或者使用者并不关心的非结果部分，我们称之为隐藏层

在实际的网络模型中，隐藏层会有非常多的层数，它们是网络最为关键的内部核心，也是模型能够学习知识的关键部分

在图的右侧，蓝色的神经元是网络的最后一层。模型内部计算完成之后，就需要通过这一层输出到外部，所以也叫做输出层

需要说明的是，神经元之间的连线，表示神经元之间连接的权重，通过权重就会知道网络中每个节点的重要程度

那么现在我们回头再来看看前馈神经网络这个名字，是不是就很好理解了。在前馈网络中，数据从输入层进入到隐藏层的第一层，然后传播到第二层，第三层...一直到最后通过输出层输出。数据的传播是单向的，无法后退，只能前行

导数、梯度与链式法则

既然有了前向的数据传播，自然也会有反向的数据传播过程

说到反向传播，我们常常会听到梯度下降、链式法则等

接下来我们来回顾下高数学过的导数、偏导数，搞懂这些前置知识，就能对反向传播所需的知识做一个回顾，也能更好地理解反向传播的原理

导数

当然，有的函数不止一个变量，比如z=3x+2y，这个函数中就同时存在了x和y两种变量，那该怎么求它们的导数呢？

这时我们就要让偏导数登场了。偏导数其实就是保持一个变量变化，而所有其他变量恒定不变的求导过程

假设有个函数z=f(x,y)，当我们要求x方向的导数的时候，就可以给x一个非常小的增量Δx，同时保持y不变。反之，如果要求y方向的导数，则需要给y一个非常小的增量Δy，而x保持不变。于是就能得出如下的偏导数描述公式：

$\frac{\partial}{\partial_{x_j}} f(x_0,x_1,...,x_n) = \displaystyle\lim_{\triangle x \to 0} \frac{\triangle y}{\triangle x} = \displaystyle\lim_{\triangle x \to 0} \frac { f(x_0,...,x_j + \triangle x , ... , x_n) - f (x_0, ... , x_j, ... , x_n) }{\triangle x}$

上面的公式，看上去很复杂，其实仔细看，只有$x_j$​这个变量有一个小小的Δx，也就是说在x的某一个维度(j)增加了一个小的增量

比如对于函数 $z = x^2 + y^2$，$\frac{\partial_z}{\partial_x} = 2x$表示函数z在x上的导数，$\frac{\partial_z}{\partial_y} = 2y$表示函数z在y上的导数

梯度

当我们了解了导数和偏导数的概念之后，那么梯度的概念就会非常容易理解了。函数所有偏导数构成的向量就叫做梯度

我们一般使用∇f来表述函数的梯度。它的描述公式为：

$\nabla f(x) = [ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2} , ... , \frac{\partial f}{\partial x_i} ]$

关于梯度，后面这个结论一定要牢记：梯度向量的方向即为函数值增长最快的方向

这是一个非常重要的结论，它贯穿了整个深度学习的全过程。模型要学习知识，就要用最快最好的方式来完成，其实就是需要借助梯度来进行。不过，这个结论涉及的证明过程以及数学知识点非常多，只需要记住结论就够了

链式法则

深度学习的整个学习过程，其实就是一个更新网络节点之前权重的过程。这个权重就是刚才在前馈网络中示意图中看到的节点之间的连线，权重我们一般使用w来进行表示

模型就是通过不断地减小损失函数值的方式来进行学习的。让损失函数最小化，通常就要采用梯度下降的方式，即：每一次给模型的权重进行更新的时候，都要按照梯度的反方向进行

为什么呢？因为梯度向量的方向即为函数值增长最快的方向，反方向则是减小最快的方向

这个内容比较重要，我们换个方式再说一次：模型通过梯度下降的方式，在梯度方向的反方向上不断减小损失函数值，从而进行学习

假设我们把损失函数表示为：

$H(W_{11}, W_{12}, ... , W_{ij} , ... , W_{mn})$

其中，$W_{ij}$表示第i层的第j个节点对应的权重值。则其梯度向量▽H为：

$[ \frac{\partial H}{\partial w_{11}}, \frac{\partial H}{\partial w_{12}}, ... \frac{\partial H}{\partial w_{ij}}, ... \frac{\partial H}{\partial w_{mn}}]$

感觉这个公式好复杂啊，令人头秃。就比如第一项，$w_{11}$跟H的关系我哪知道呀，中间隔了那么多层

这时候，就需要链式法则隆重登场了：“两个函数组合起来的复合函数，导数等于里面函数代入外函数值的导数，乘以里面函数之导数。”这个法则包括了两种形式：

$\frac{dy}{dx} = f'(g(x))g'(x)$

$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$

举例，假设我们手中有函数$f(x)= \cos (x^2 - 1)$。我们可以把函数分解为：

f(x) = cos(x)

$g(x) = x^2 - 1$

g(x)的导数g'(x) = 2x，f(x)的导数f'(x) = -sin(x)，则 $f'(x) = f'(g(x))g'(x) = -sin (x^2 - 1)2x$，相当于各自求导后再相乘

反向传播

了解了导数、偏导数、梯度、链式法则，我们就能来学习反向传播了

反向传播算法（Backpropagation）是目前训练神经网络最常用且最有效的算法。模型就是通过反向传播的方式来不断更新自身的参数，从而实现了“学习”知识的过程

反向传播的主要原理是：

• 前向传播：数据从输入层经过隐藏层最后输出，其过程和之前讲过的前馈网络基本一致
• 计算误差并传播：计算模型输出结果和真实结果之间的误差，并将这种误差通过某种方式反向传播，即从输出层向隐藏层传递并最后到达输入层
• 迭代：在反向传播的过程中，根据误差不断地调整模型的参数值，并不断地迭代前面两个步骤，直到达到模型结束训练的条件

其中最重要的环节有两个：一是通过某种方式反向传播；二是根据误差不断地调整模型的参数值

这两个环节，我们统称为优化方法，一般而言，多采用梯度下降的方法。这里就要使用到导数、梯度和链式法则相关的知识点

反向传播的数学推导以及证明过程是非常复杂的，在实际的研发过程中反向传播的过程已经被PyTorch、TensorFlow等深度学习框架进行了完善的封装

所以我们不需要手动去写这个过程。不过作为深度学习的研发人员，我们还是需要了解这个过程的运转方式，这样才能搞清楚深度学习中模型具体是如何学习的

用下山路线规划理解优化方法

优化方法，指的是一个过程，这个过程的目的就是，寻找模型在所有可能性中达到评估效果指标最好的那一个。我们举个例子，对于函数f(x)，它包含了一组参数

这个例子中，优化方法的目的就是找到能够使得f(x)的值达到最小值对应的权重。换句话说，优化过程就是找到一个状态，这个状态能够让模型的损失函数最小，而这个状态就是模型的权重

常见的优化方法种类非常多，常见的有梯度下降法、牛顿法、拟牛顿法等，涉及的数学知识也更是不可胜数。同样的，PyTorch也将优化方法进行了封装，我们在实际开发中直接使用即可，节省了大量的时间和劳动

不过，为了更好地理解深度学习特别是反向传播的过程，我们还是有必要对一些重要的优化方法进行了解

其中，梯度下降法，是深度学习中使用最为广泛的优化方法。梯度下降其实很好理解，我们以下山路线规划为例来理解梯度下降

假如你和朋友去爬山，到了山顶之后忽然想上厕所，需要尽快到达半山腰的卫生间，这时候你就需要规划路线，该怎么规划呢？

在不考虑生命危险的情况下，那自然是怎么快怎么走了，能跳崖我们绝不走平路，也就是说：越陡峭的地方，就越有可能快速到达目的地

所以，我们就有了一个送命方案：每走几步，就改变方向，这个方向就是朝着当前最陡峭的方向，即坡度下降最快的方向行走，并不断重复这个过程。这就是梯度下降的最直观的表示了

下面我们用相对严谨的方式来表述梯度下降：

在一个多维空间中，对于任何一个曲面，我们都能够找到一个跟它相切的超平面。这个超平面上会有无数个方向

但是这所有的方向中，肯定有一个方向是能够使函数下降最快的方向，这个方向就是梯度的反方向。每次优化的目标就是沿着这个最快下降的方向进行，就叫做梯度下降

具体来说，在一个三维空间曲线中，任何一点我们都能找到一个与之相切的平面（更高维则是超平面），这个平面上就会有无穷多个方向，但是只有一个使曲线函数下降最快的梯度

总之：每次优化就沿着梯度的反方向进行，就叫做梯度下降。使什么函数下降最快呢？答案就是损失函数

图中红色的线路，是一个看上去还不错的上厕所的路线。但是我们发现，还有别的路线可选。不过，下山就算是不要命地跑，也得讲究方法

就比如，步子大小很重要，太大的话你可能就按照上图中的黄色路线跑了，最后跑到了别的山谷中（函数的局部极小值而非整体最小值）或者在接近和远离卫生间的来回震荡过程中，结果可想而知

但是如果步伐太小了，则需要的时间就很久，可能你还没走到目的地，就坚持不住了（蓝色路线）

在算法中，这个步子的大小，叫做学习率（learning rate）。因为步长的原因，理论上我们是不可能精确地走到目的地的，而是最后在最小值的某一个范围内不断地震荡，也会存在一定的误差，不过这个误差是我们可以接受的

在实际的开发中，如果损失函数在一段时间内没有什么变化，我们就认为是到达了需要的“最低点”，就可以认为模型已经训练收敛了，从而结束训练

常见的梯度下降方法

我们搞清楚了梯度下降的原理之后，下面具体来看几种最常用的梯度下降优化方法

批量梯度下降法（Batch Gradient Descent，BGD）

线性回归模型是我们最常用的函数模型之一。假设对于一个线性回归模型，y是真实的数据分布函数

$h_{\theta} = \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n$

是我们通过模型训练得到的函数，其中θ是h的参数，也是我们要求的权值

损失函数J(θ)可以表述为如下公式：

$cost = J(\theta) = \frac{1}{2m} \displaystyle \sum_{i=1}^m(h_{\theta}(x^i) - y^i)^2$

在这里，m表示样本数量。既然要想损失函数的值最小，我们就要使用到梯度，让损失函数以最快的速度减小，就得用梯度的反方向

首先我们对J(θ)中的θ求偏导数，这样就可以得到每个θ对应的梯度：

$\frac{\partial J (\theta)}{ \partial \theta_j} = - \frac{1}{m} \displaystyle \sum_{i=1}^m (h_{\theta}(x^i)-y^i)x_j^i$

得到了每个θ的梯度之后，我们就可以按照下降的方向去更新每个θ，即：

$\theta_j' = \theta_j - \alpha \frac{1}{m} \displaystyle \sum_{i=1}^{m} (h_{\theta}(x^i)-y^i)x_j^i$

其中α就是我们刚才提到的学习率。更新θ之后，我们就得到了一个更新之后的损失函数，它的值肯定就会更小，那么我们的模型就更加接近于真实的数据分布了

在上面的公式中，你注意到了m这个数了吗？没错，这个方法是当所有的数据都经过了计算之后再整体除以它，即把所有样本的误差做平均

这里我想提醒你，在实际的开发中，往往有百万甚至千万数量级的样本，那这个更新的量就很恐怖了。所以就需要另一个办法，随机梯度下降法

随机梯度下降（Stochastic Gradient Descent，SGD）

随机梯度下降法的特点是，每计算一个样本之后就要更新一次参数，这样参数更新的频率就变高了。其公式如下：

$\theta_j' = \theta_j - \alpha (h_{\theta}(x^i)-y^i)x_j^i$

想想看，每训练一条数据就更新一条参数，会有什么好处呢？有的时候，我们只需要训练集中的一部分数据，就可以实现接近于使用全部数据训练的效果，训练速度也大大提升

然而，鱼和熊掌不可兼得，SGD虽然快，也会存在一些问题。就比如，训练数据中肯定会存在一些错误样本或者噪声数据

那么在一次用到该数据的迭代中，优化的方向肯定不是朝着最理想的方向前进的，也就会导致训练效果（比如准确率）的下降，最极端的情况下，就会导致模型无法得到全局最优，而是陷入到局部最优

世间安得两全法，有的时候舍弃一些东西，我们才能获得想要的。随机梯度下降方法选择了用损失很小的一部分精确度和增加一定数量的迭代次数为代价，换取了最终总体的优化效率的提高

当然这个过程中增加的迭代次数，还是要远远小于样本的数量的

那如果想尽可能折衷地去协调速度和效果，该怎么办呢？我们很自然就会想到，每次不用全部的数据，也不只用一条数据，而是用“一些”数据，这就是接下来我们要说的小批量梯度下降

小批量梯度下降（Mini-Batch Gradient Descent, MBGD）

Mini-batch的方法是目前主流使用最多的一种方式，它每次使用一个固定数量的数据进行优化

这个固定数量，我们称它为batchsize。batchsize较为常见的数量一般是2的n次方，比如32、128、512等

batchsize太小的话，那么每个batch之间的差异就会很大，迭代的时候梯度震荡就会严重，不利于收敛

batchsize越大，那么batch之间的差异越小，梯度震荡小，利于模型收敛

但是凡事有个限度，如果batchsize太大了，训练过程就会一直沿着一个方向走，从而陷入局部最优

这也就是为什么我们要不断的尝试一个相对合理的minibatch

其实具体的数值设成为多少，也需要根据项目的不同特点，采用经验或不断尝试的方法去进行设置，比如图像任务batchsize我们倾向于设置得稍微小一点，NLP任务则可以适当的大一些

基于随机梯度下降法，人们又提出了包括momentum、nesterov momentum等方法，点击这里