初等变换 & 矩阵的秩

初等变换

• 交换两行
• 用k（k!=0）乘以某一行
• 某一行的k倍加到另一行上去

初等列变换

• 交换两列
• 用k（k!=0）乘以某一列
• 某一列的k倍加到另一列上去

本质：对矩阵的一种变化

• 交换两行：A->B，|A|=-|B|
• 用k（k!=0）乘以某一行：A->B，k|A|=|B|
• 某一行的k倍加到另一行上去：A->B，|A|=|B|

A经过初等变换得到B，叫作：A和B等价，A等价于B

反身性：A经过初等变换得到A，A等价于A

对称性：A和B等价，则B和A也等价

传递性：A等价于B，B等价于C，那么A也等价于C

任何矩阵A都等价于标准形

初等方阵

E(i,j)表示交换第i行（列）和第j行（列），|E(i,j)|=-1

E(i(k)) （k!=0）表示第i行乘以k倍，|E(i(k))|=k

E(i,j(k))，j行乘以k倍加到i行去，|E(i,j(k))|=1

$E^{-1}(i,j)=E(i,j)$

$E^{-1}(i(k))=E(i(\frac{1}{k}))$

$E^{-1}(i,j(k))=E(i,j(-k))$

$E(2(3)) = \begin{bmatrix} 1&0&0\\ 0&3&0\\ 0&0&1 \end{bmatrix}$

$E(1,3) = \begin{bmatrix} 0&0&1\\ 0&1&0\\ 1&0&0 \end{bmatrix}$

$A = \begin{bmatrix} 1&2&3\\ 4&5&6\\ 7&8&9 \end{bmatrix}$

$E(2(3))A = \begin{bmatrix} 1&2&3\\ 12&15&18\\ 7&8&9 \end{bmatrix}$

$AE(1,3) = \begin{bmatrix} 3&2&1\\ 6&5&4\\ 9&8&7 \end{bmatrix}$

定理3：任意矩阵A都存在初等矩阵 $P_1,P_2,...,P_s \quad Q_1,Q_2,...,Q_t$，使得$P_s,...,P_2P_1 A Q_1,Q_2,...,Q_t$为标准形

证明：根据前面的定理（任何矩阵都能通过初等变换化为标准形）以及上面的初等方阵（左乘、右乘），可以理解为对A做了一系列初等行、列变换后变化为了标准形

推论：如果A、B等价 <=> 存在可逆矩阵P、Q，使得PAQ=B

证明：跟定理3的证明类似，一系列初等矩阵相乘可以得到可逆矩阵P、Q（初等矩阵均可逆）

定理4：A可逆 <=> A的标准形为E

证明：两边同时取行列式，得：$|P_s|,...,|P_2||P_1| |A| |Q_1|,|Q_2|,...,|Q_t| = |D|$

因为A可逆，以及左边的一系列初等矩阵也都可逆，所以左边的行列式的乘积必定不等于0，所以右边的行列式也不能等于0

所以A的标准形只能为单位阵E（对角线上如果有一个0，那么整个行列式就等于0，等式就不成立）

定理5：A可逆 <=> A可以表示成一些初等矩阵的乘积（$A=P_1P_2...P_s$）

初等变换法求逆矩阵

$(A,E) = \begin{bmatrix} 1&0&1&1&0&0\\ 2&1&0&0&1&0\\ -3&2&-5&0&0&1 \end{bmatrix} -> \begin{bmatrix} 1&0&0&{-\frac{5}{2}}&1&{-\frac{1}{2}}\\ 0&1&0&5&{-1}&1\\ 0&0&1&{\frac{7}{2}}&{-1}&{\frac{1}{2}} \end{bmatrix}$

把A转成单位阵后，右边的部分就是$A^{-1}$

$(A,E) = \begin{bmatrix} 1&2&3\\ 2&4&9\\ 4&8&18 \end{bmatrix}$

矩阵的秩

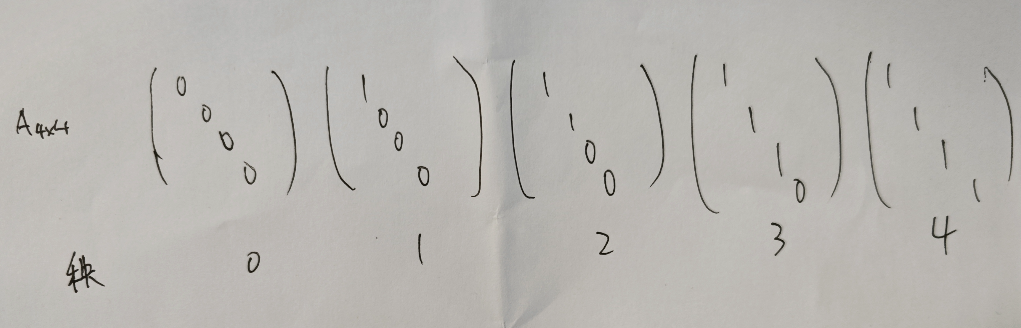
k阶子式

秩(A) = 5 也可以用 r(A) = 5 表示，r是rank的缩写

r(0) = 0

$A_{m \times n} \quad$ 0 <= r(A) <= min(m,n)

r(A)=m，表示取了所有行，叫作：行满秩

r(A)=n，表示取了所有列，叫作：列满秩

统称：满秩

r(A) < min(m,n)，表示不是满秩，叫作：降秩

定理1：r(A)=r <=> 有一个r阶子式不为0而所有的r+1阶子式全为0

举例：$r(A_{6\times8})=3$ <=> 3阶子式不为0，4阶子式全为0

性质1：$r(A)=r(A^T)$

性质2：任意矩阵乘以可逆矩阵，秩不变

性质3：$A_{m \times n}$，P是m阶可逆方阵，Q是n阶可逆方阵，那么：r(A)=r(PA)=r(AQ)=r(PAQ)（左乘一个可逆矩阵或右乘一个可逆矩阵或左右都乘一个可逆矩阵，秩不变）

阶梯形矩阵

若有0行，0行在非0行的下面

自上而下，左起的首个非0元素的左边0的个数随行数增加而严格增加

严格：楼梯不能一次走2格，即：每次必须增加（不能相等）

$YES = \begin{bmatrix} 1&1&1&1&1&1\\ 0&1&2&3&4&1\\ 0&0&0&1&1&1\\ 0&0&0&0&0&1\\ 0&0&0&0&0&0 \end{bmatrix}$

$NO = \begin{bmatrix} 1&1&1&1&1\\ 0&1&1&1&1\\ 0&0&0&1&1\\ 0&0&0&3&4\\ 0&0&0&0&0 \end{bmatrix}$

矩阵的秩等于非0行的行数

初等变换不改变矩阵的秩

A -> 初等行（列）变换（建议统一用行变换） -> 阶梯形（非0行的行数就是矩阵的秩）

变换步骤：先处理第1列再处理第2列，依次类推（如果步骤中关键元素是0，先把0相关的行交换下去）

行简化阶梯形矩阵

1. 非0行的首个非0元素是1
2. 首非0元所在列的其余元素是0

$\begin{bmatrix} 1&0&0&4\\ 0&1&0&5\\ 0&0&1&4\\ 0&0&0&0 \end{bmatrix}$