连续值的概率分布

累积分布函数的预热

假设有一条由打印机从左至右打印出的渐变色带。我们设色带长10cm，最终消耗的油墨总量为1mg。如图4.1所示

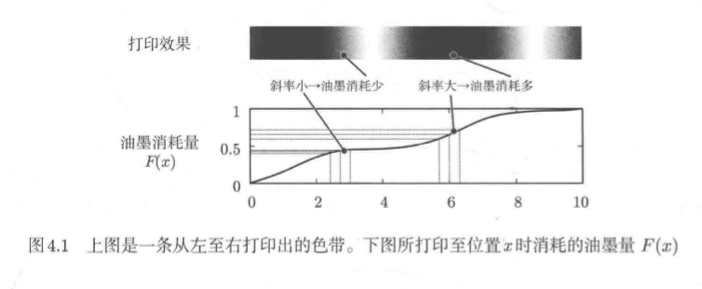
从图中可以看出，从x=a至x=b的油墨消耗量为F(b)-F(a)(a<=b)

概率密度函数预热

图4.2添加了表示位置x处油墨浓度的函数f(x)。F(x)的斜率越大，f(x)的值也越大

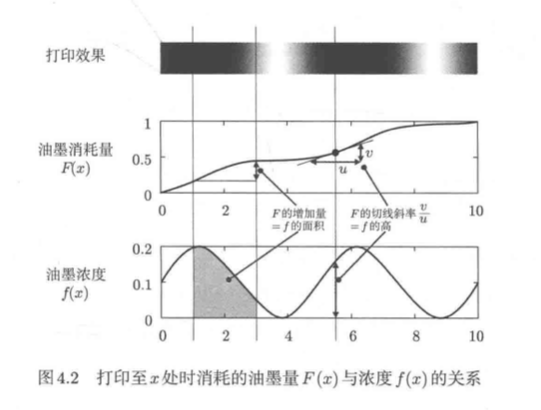
F与f的关系可以像这样通过微积分表示。事实上，浓度f(x)由x自增时F(x)的增量决定，而这正是微分的概念

$f(x) = F'(x) = \frac{dF(x)}{dx}$

通常，如果f是F的微分，F同样能通过f的积分得到

$\int_a^b{f(x)dx = F(b) - F(a)}$

如图4.3所示，色带左侧4cm长的部分均匀喷上了0.6mg的油墨，也就是说，每1cm喷有0.6/4=0.15mg的油墨，于是，我们称油墨的密度为0.15mg/cm

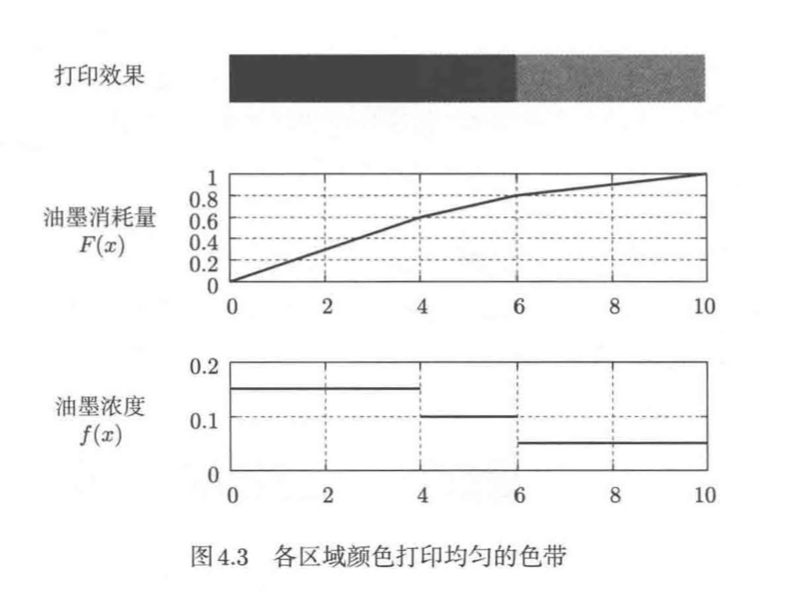
所有三个部分的密度如下：

• 左侧：长4cm的色带喷了0.6mg的油墨......密度0.6/4=0.15mg/cm
• 中间：长2cm的色带喷了0.2mg的油墨......密度0.2/2=0.1mg/cm
• 右侧：长4cm的色带喷了0.2mg的油墨......密度0.2/4=0.05mg/cm

由此可得，油墨消耗量/长度=密度

同理，长度×密度=油墨消耗量

变量变换的预热

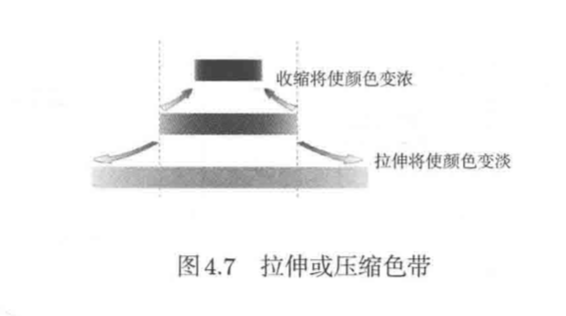
这条色带并非纸质，而是一条透明的橡胶带。由于是橡胶材质，我们自然可以像图4.7那样对其做拉伸或压缩处理

如果长度拉伸为原来的两倍，油墨的浓度就会下降为原来的一半

反之，如果长度压缩为原来的一半，油墨浓度则将翻倍

通常，如果油墨的喷印量不变，色带宽度变为原来的α倍，密度就会变为原来的1/α倍

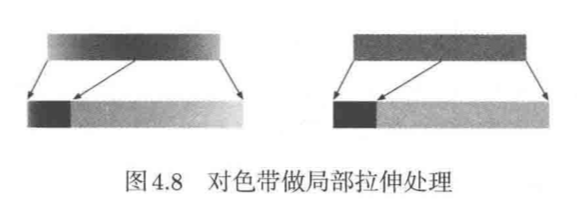
我们不仅可以均匀拉伸整条色带，使其长度变为原来的α倍，也可以对色带做局部拉伸处理

图4.8是色带左半部分压缩右半部分拉伸后的结果。左半部分在长度压缩为原来的一半后密度倍增，右半部分在长度翻倍后密度减半

现在，让我们进一步分析已有的观察结果。我们希望通过原来的位置x与变形后的位置y求出油墨浓淡的变化关系式

首先考虑整条色带均匀拉伸至原长两倍的情况，即y=2x，如图4.10左：

类似地，如果整条色带均匀压缩至原来的一半，即y=x/2，如图4.10右：

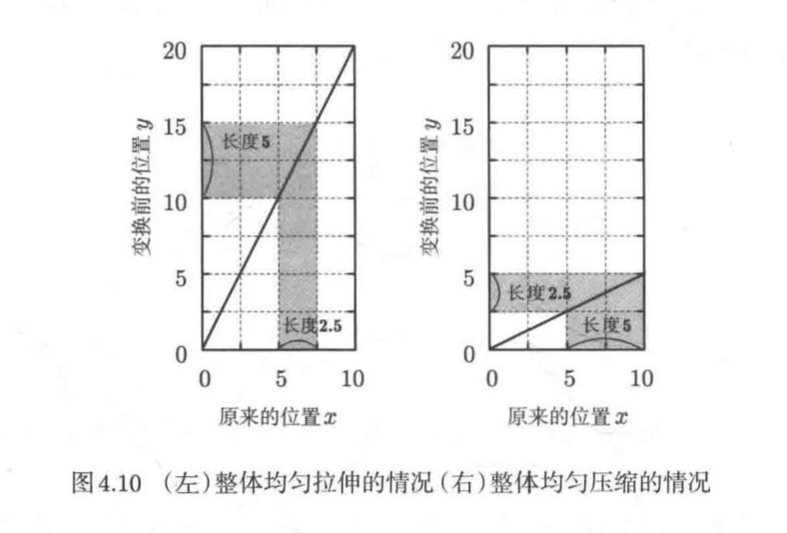
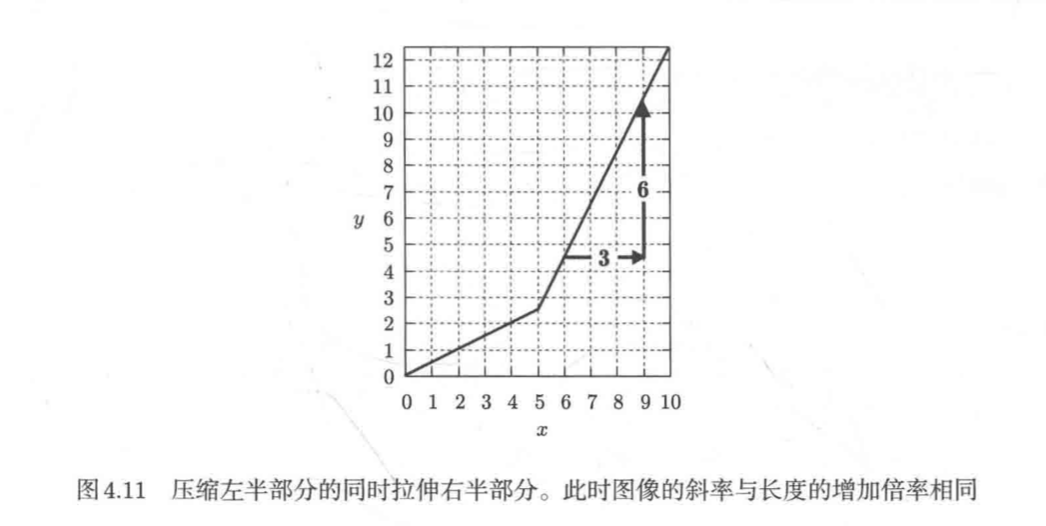
图4.11是由色带左半部分压缩右半部分拉伸得到的转换图像

从该图可以看出，色带的左半部分压缩至了原长的一半，而右半部分则拉伸至了原长的两倍

例如，变换之前，x=6至x=9之间的长度为3，变换之后，y=4.5至y=10.5之间的长度为6，长度增加了6/3=2倍。因此，这段色带的密度是原来的1/2

长度的变化比例与图像斜率的计算方式相同。由于长度从3增加至了6，因此斜率即为6/3=2

推而广之，对于任何情况，我们都可以通过图像的斜率来表示喷印长度的变化比例

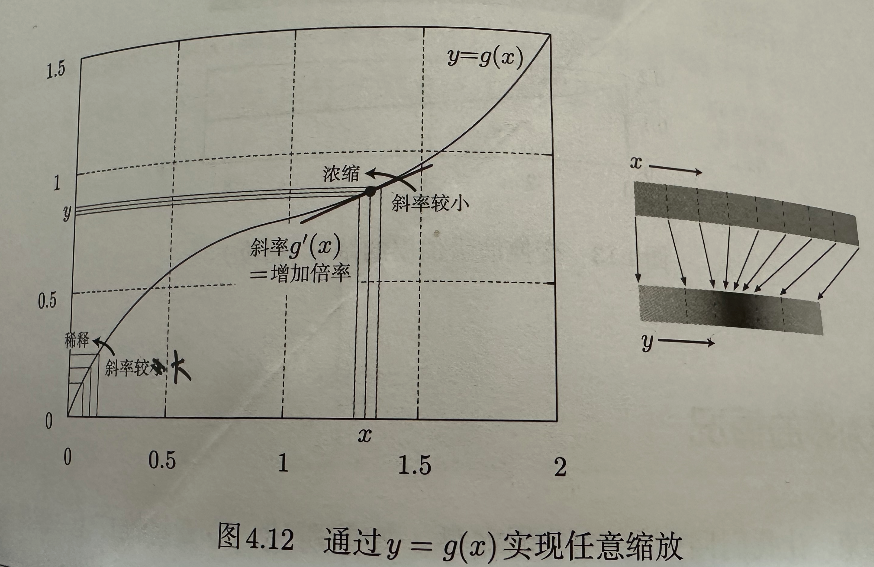
接下来，我们将开始讨论问题的本质。先来看一下对于任意的函数g，经过变形y=g(x)后密度将如何变化，如图4.12所示

问题的关键是图像的斜率。如果某处的斜率为α，该处附近的长度就会是原来的α倍，于是密度变为原来的1/α倍

我们可以通过变换式g(x)的微分g'(x)求得斜率α的值

设原本位置x处的油墨密度为f(x)，变形后的位置y=g(x)处的油墨密度将是原来的$\vert 1/g'(x) \vert$倍

我们也可以通过以下形式表示油墨密度，$\vert \frac{f(x)}{g'(x)} \vert$

为什么一定要使用绝对值

对于长度，似乎负数也不会有什么问题。例如，变换式g(x)=-2x，表示翻转色带后再扩大两倍

然而，油墨的浓度无法为负值。因此我们不能用1/(-2)来表示浓度的倍率，而必须使用$1 / \vert -2 \vert$

练习题 4.1

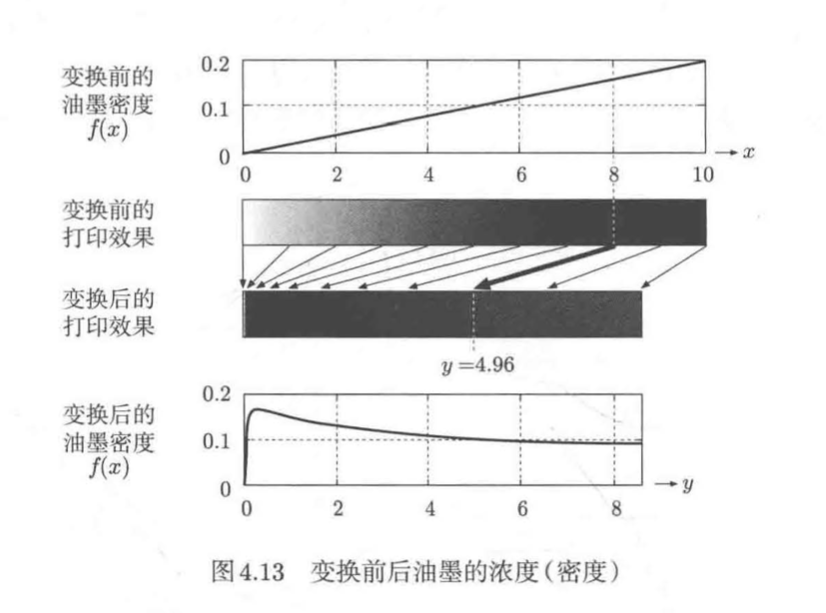
请根据以下条件计算变换后位置y=4.96处的油墨密度（提示：4.96=g(8)）

• 油墨的密度f(x)=0.02x（0<=x<=10）
• 变换$y=g(x)=0.005x^3+0.03x^2+0.06x$

由提示可知，与y=4.96对应的是x=8。又由 $g'(x)=0.015x^2+0.06x+0.06$ 得 g'(x)=1.5

因此，变换后y=4.96处的密度为 $\vert f(8)/g'(8) \vert = \vert 0.16/1.5 \approx 0.11 \vert$

概率为零的情况

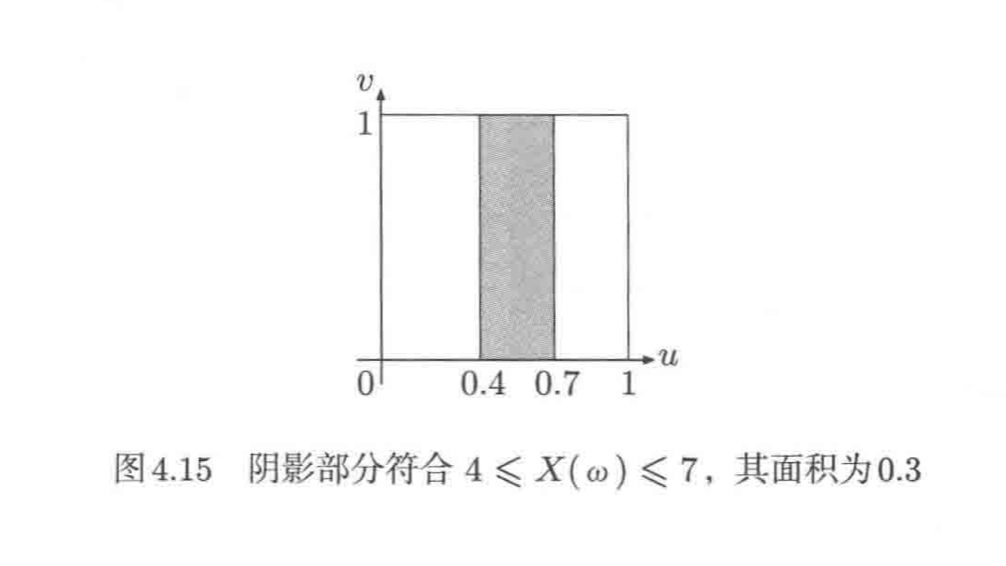
概率可以通过面积计算。例如，X大于等于4且小于等于7的概率为0.3。这是因为，满足4 <= X(ω) <= 7的ω=(u,v)正好是图4.15中的阴影部分

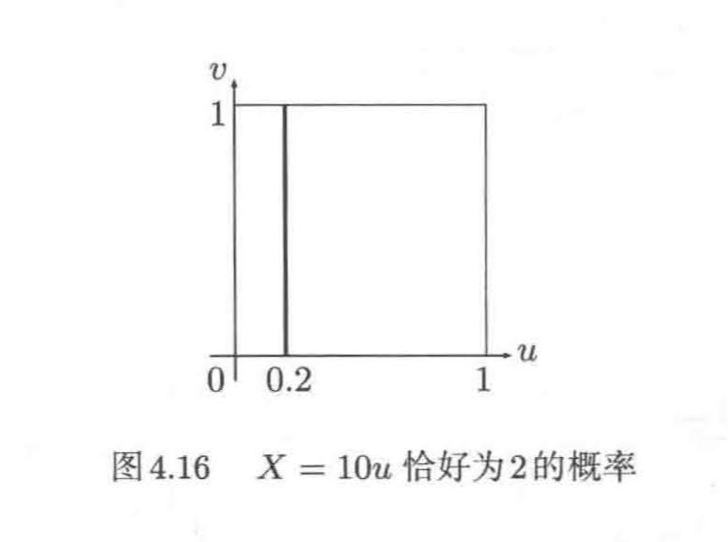
接下来进入正题。X的值恰好为2的概率P(X=2)是多少呢？满足X(ω)=2的点ω的集合可以由图4.16中的线段表示

由于这条线段的面积为0，所以，P(X=2)=0

因为在实数范围内，这个线上的点有无数个，所以在线上取一个点的概率最终将趋近于0

因此，即使X的取值落在某一范围内的概率为正，X恰好为某个值的概率也必然为零。两者并不矛盾，这是概率论中的客观事实

累积分布函数与概率密度函数

实数值随机变量的概率分布(各个值的出现概率)应该如何表述呢?我们只要将"概率密度函数预热"中的"油墨"理解为"概率"，情况便一目了然了

图4.20的左半部分是油墨的消耗情况。从图中可以看到，某些位置的油墨消耗量也恰好为零。不过这不妨碍我们描述油墨的打印效果，油墨消耗量与浓度的图像依然能表述所需的信息

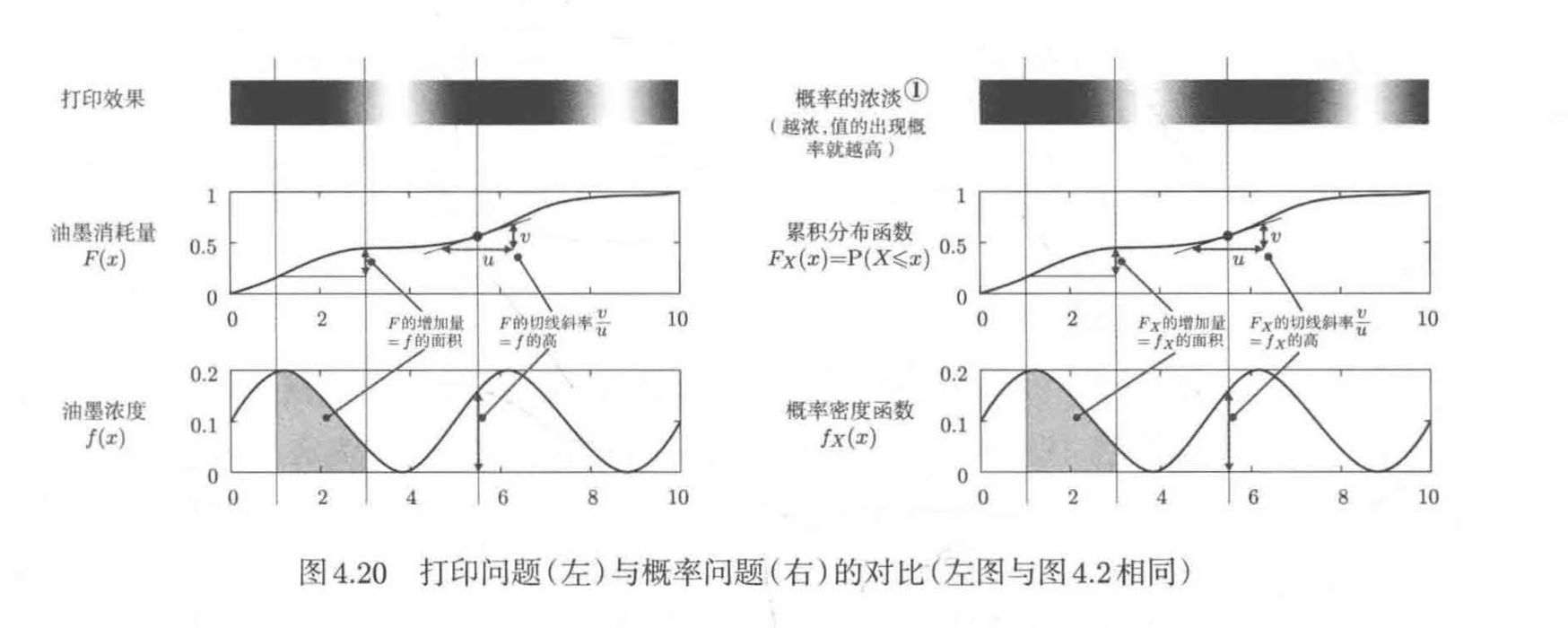
现假设X是一个实数值随机变量，并将油墨消耗量视作X的取值概率。如图4.20右。直至位置a处的油墨量F(a)与直至a处的概率之和P(X<=a)对应

我们将其称为累积分布函数(或简称为分布函数)，其数学定义如下：

$F_x(a) \equiv P(X \leq a)$

如果进一步微分消耗的油墨量F(x)，就能得到油墨的浓度。同理，只要微分累积分布函数，就能得到概率的浓度(即密度)

$f_x(x) \equiv F'_x(x) = \frac{dF_x(x)}{dx}$

$f_x(x)$称为概率密度函数。概率密度函数$f_x(x)$的值越大，x附近的概率就越浓，也就是说，x附近的值有着更高的出现概率

事实上，某一位置(如x加减0.1的范围内)密度越大就表示油墨量越多。用概率来解释，就是x加减0.1的范围内的值有着更高的出现概率

下表列出了两者的对应关系

我们可以通过累积分布函数与概率密度函数的图像来表示实数值的概率分布。如果条件允许，还可以用数式替代图像来表示分布

它们的形式由具体的分布决定，因此严格来讲，$f_x(x)$是"随机变量X分布的概率密度函数"

不过这种说法比较拗口，今后我们将在不会引起歧义的前提下简称为"随机变量X的概率密度函数"

在很多实际应用中，概率密度函数比累积分布函数应用范围更广。它的图像能够直接表示浓淡，更加简单明了

通过概率密度函数求解概率

那么，对于给定的概率密度函数$f_x$，我们应该如何得到指定范围内的值的出现概率呢?答案与之前求油墨浓度的方法相似

$P(a \leq X \leq b) = \int_a^b f_x(x)dx$

图4.21左是对应的图像。对于限定的范围，$f_x$的值越大，该范围对应的面积也越大，于是概率也就越大

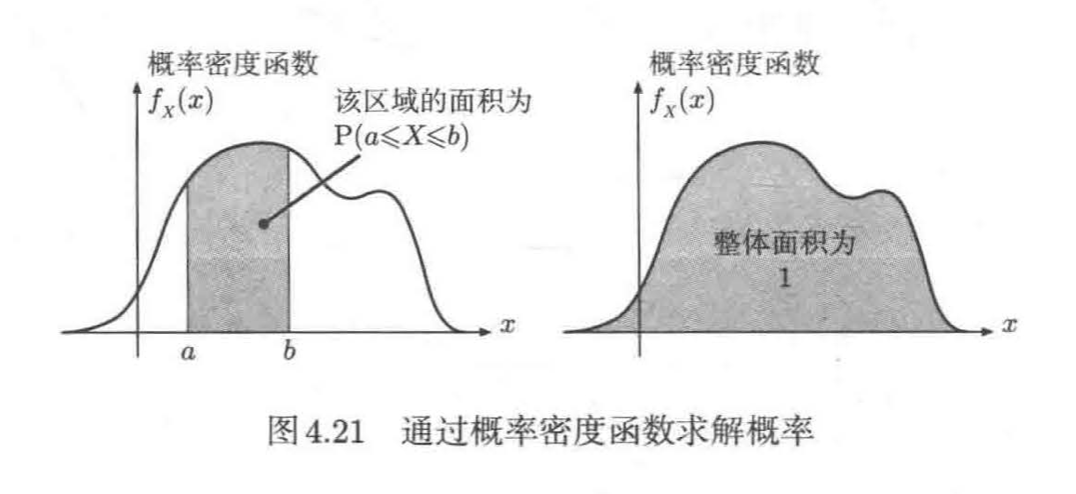
又由于一般情况下，P(-∞<X<∞)=1，因此我们能得到以下结论（图4.21右）

$\int_{-\infty}^{\infty}f_x(x)dx=1$

进一步讲，我们还能得到下面的性质

$P(X=a) = P(a \leq X \leq a) = \int_{a}^{a}f_x(x)dx=0$(无论a为何值)

在通过给定的概率密度函数来描述概率分布时，随机变量恰好为某值的概率始终为零

于是，P(a <= X < b)与P(a < X <= b)、P(a < X < b)或P(a <= X <= b)都相等

$\int_{a}^{b}f_x(x)dx$的计算结果也都相同（a<=b）

再多强调一遍，$f_x$的值并不表示"概率本身"，而是"概率的密度"

练习题 4.2

下面的不等式是否始终成立?始终成立则标为o，否则标为x

• $f_x(x) \geq 0$
• $f_x(x) \leq 1$

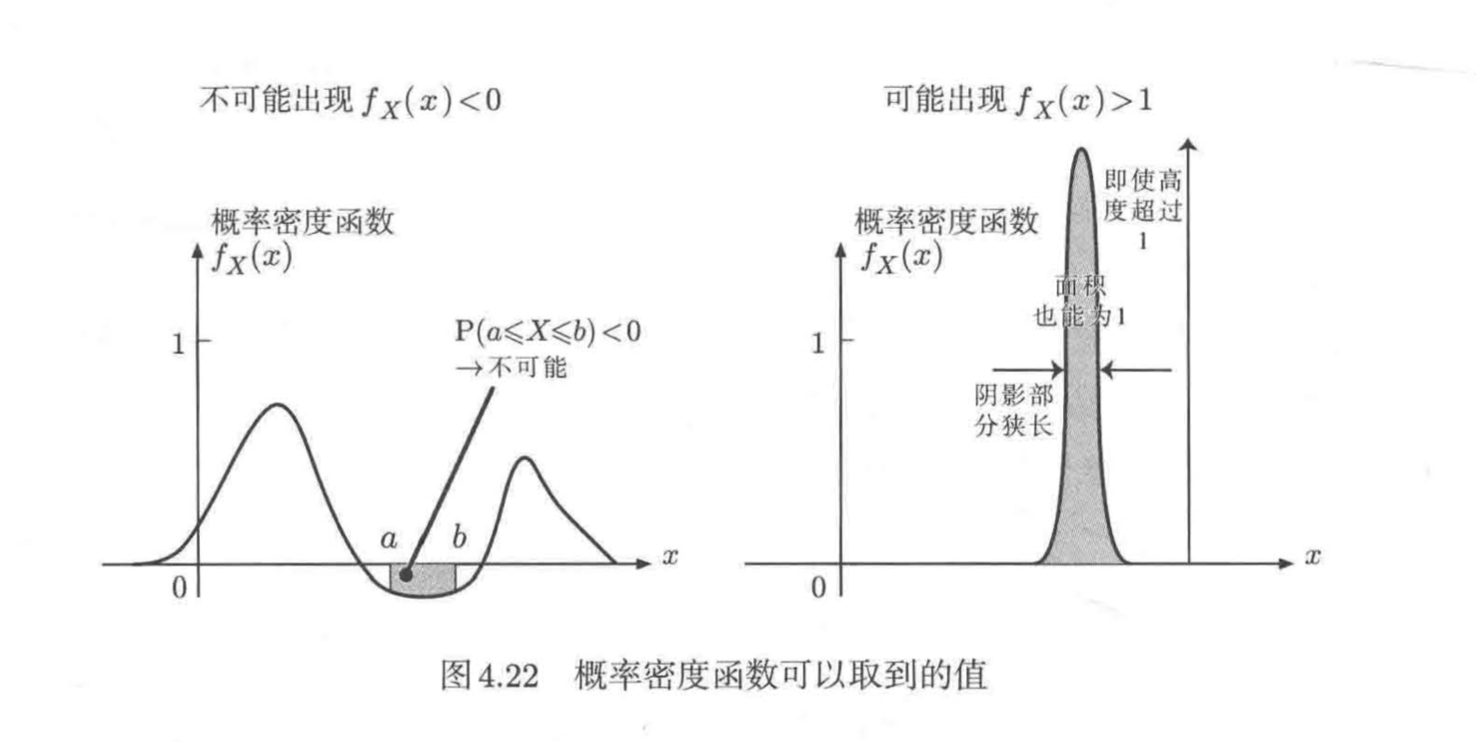
$f_x(x) \geq 0$ 正确。如果存在 $f_x(x) < 0$ 的情况，那么图4.22左，该处附近的概率将小于0，如下：

$P(a \leq X \leq b) = \int_a^b f_x(x)dx < 0$

由于概率即是面积，因此自然不可能取到负值（目前只要理解到这一层就够了）

$f_x(x) \leq 1$ 错误。如图4.22右，$f_x(x)$可以取到大于1的值。即使纵坐标高于1，整体面积也能为1

练习题 4.3

设X能够取所有实数，问下面的函数f(x)中有哪些可以作为概率密度函数

• f(x)=1
• f(x)=x
• 当0<=x<=1时，f(x)=x，否则f(x)=0
• 当x>=0时，$f(x)=e^{-x}$，否则f(x)=0
• 当-1<=x<=1时，$f(x)=1- \vert x \vert$，否则f(x)=0

能够作为概率密度函数的是4和5。2的函数值可以为负，因此不符合要求。1与3的积分(图像的面积)不为1，因此不能作为概率密度函数

练习题 4.4

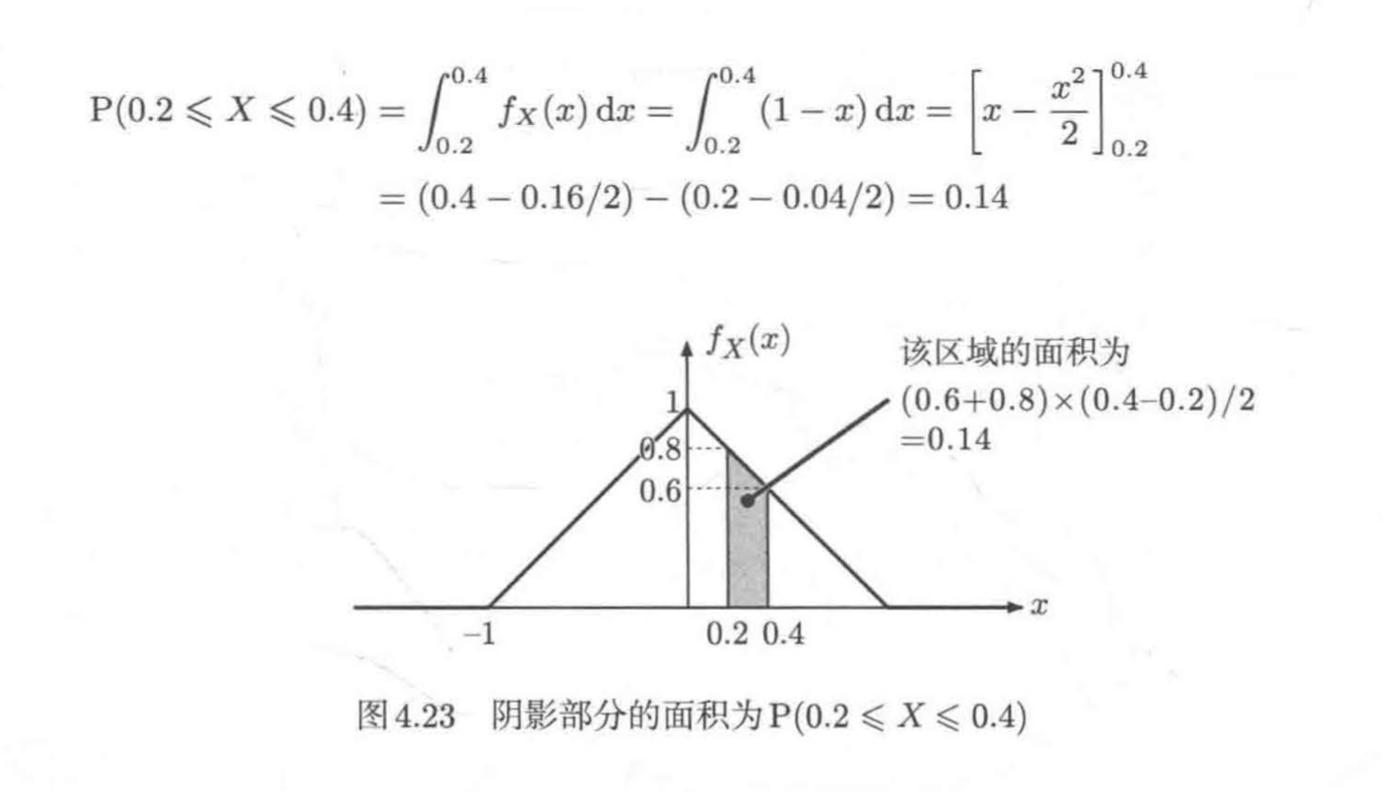
设随机变量X的概率密度函数如下。试求0.2<=X<=0.4的概率

$f(x) = \begin{cases} 1 - \vert x \vert (-1 \leq x \leq 1)\\ 0 ( x < -1 or x > 1) \end{cases}$

我们只需通过积分计算图4.23中阴影部分的面积即可，如下所示

练习题 4.5

设随机变量X的概率密度函数如下。试求在对X的小数部分做四合五人处理时，"舍去"的概率

$f(x) = \begin{cases} e^{-x} (x geq 0)\\ 0 ( x < 0) \end{cases}$

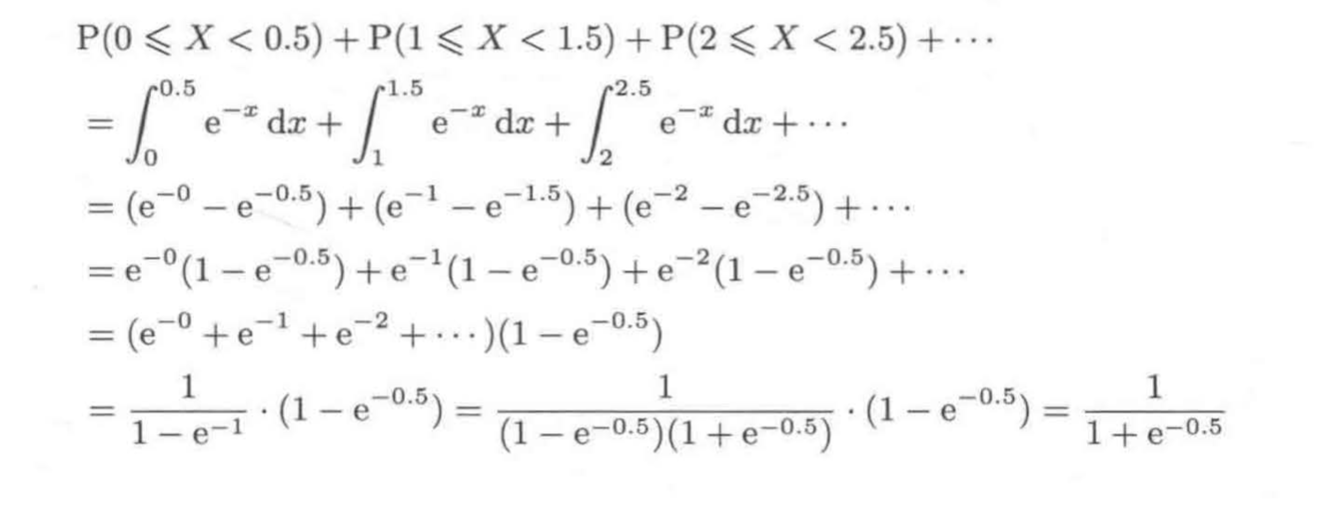
计算过程中用到了等比数列的计算公式。我们还可以通过P(入)=$e^{-0.5}$P(舍)直接得出答案

实数值的概率分布究竟是什么

实数值随机变量X的概率分布是一种特定概率的集合，这些概率满足诸如下面这样的"与X相关的条件"

• 随机变量X的值为正
• 随机变量X的值大于等于3且小于等于4
• 随机变量X的值的百位为7
• 等等等等

换言之，假设有以实数为元素的任意集合A，随机变量X的概率分布是满足以下条件的概率一览，如图4.24所示

P(X的取值属于集合A)

我们只要知道了累积分布函数与概率密度函数，就能计算得到各个相应的概率

均匀分布

在讲解离散分布时，我们介绍了均匀分布这种最为普遍的分布。类似地，实数值也定义了某一区间上的均匀分布

图4.25的概率分布由概率密度函数表述，我们称该图所示的分布为区间[α，β]上的均匀分布(α<β)

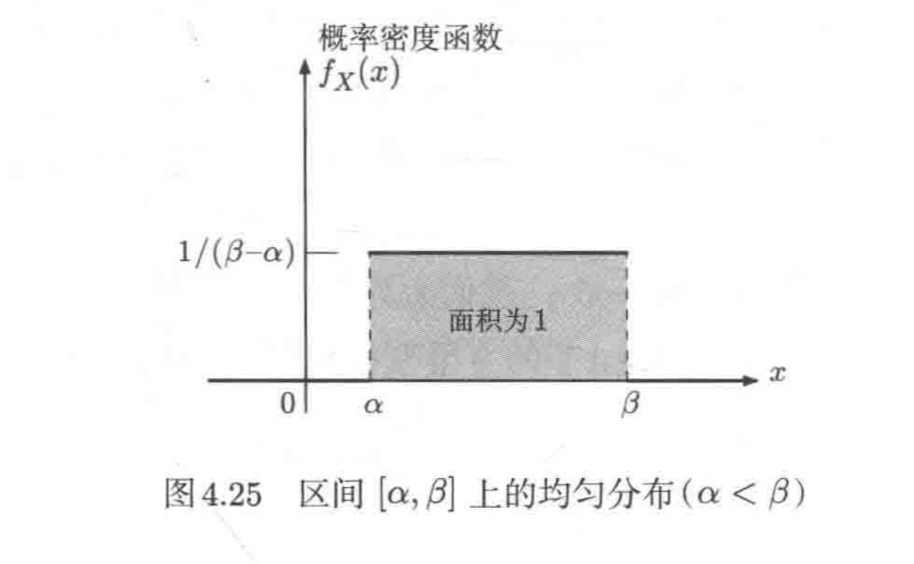
均匀分布的数学定义如下

$f(x) = \begin{cases} \frac{1}{\beta - \alpha} ( \alpha \leq x \leq \beta)\\ 0 ( \alpha \leq x \leq \beta) \end{cases}$

也就是说，均匀分布满足以下两个条件

• 区间内任意值的概率密度(出现的概率)恒定
• 不会出现区间范围之外的值