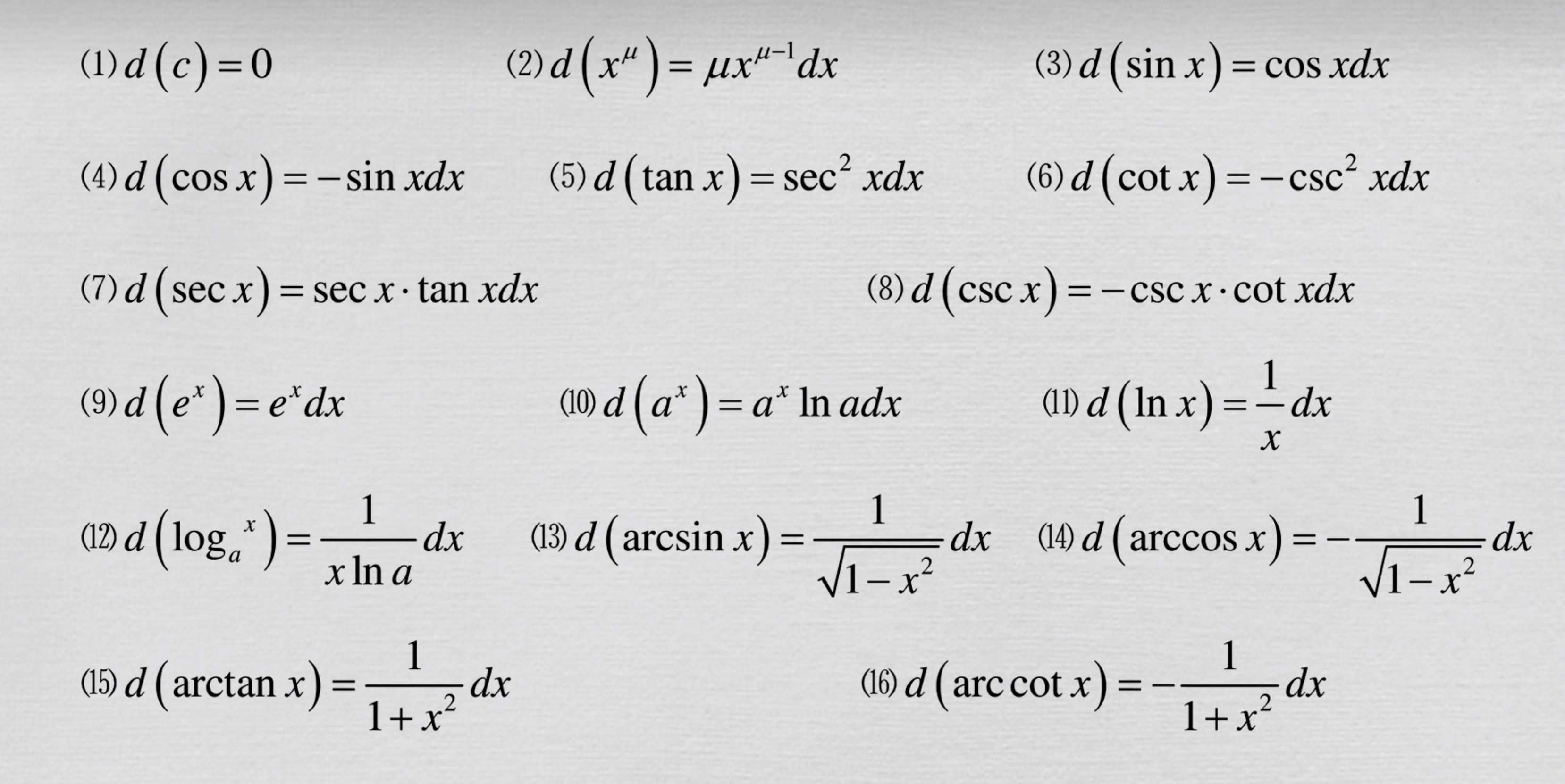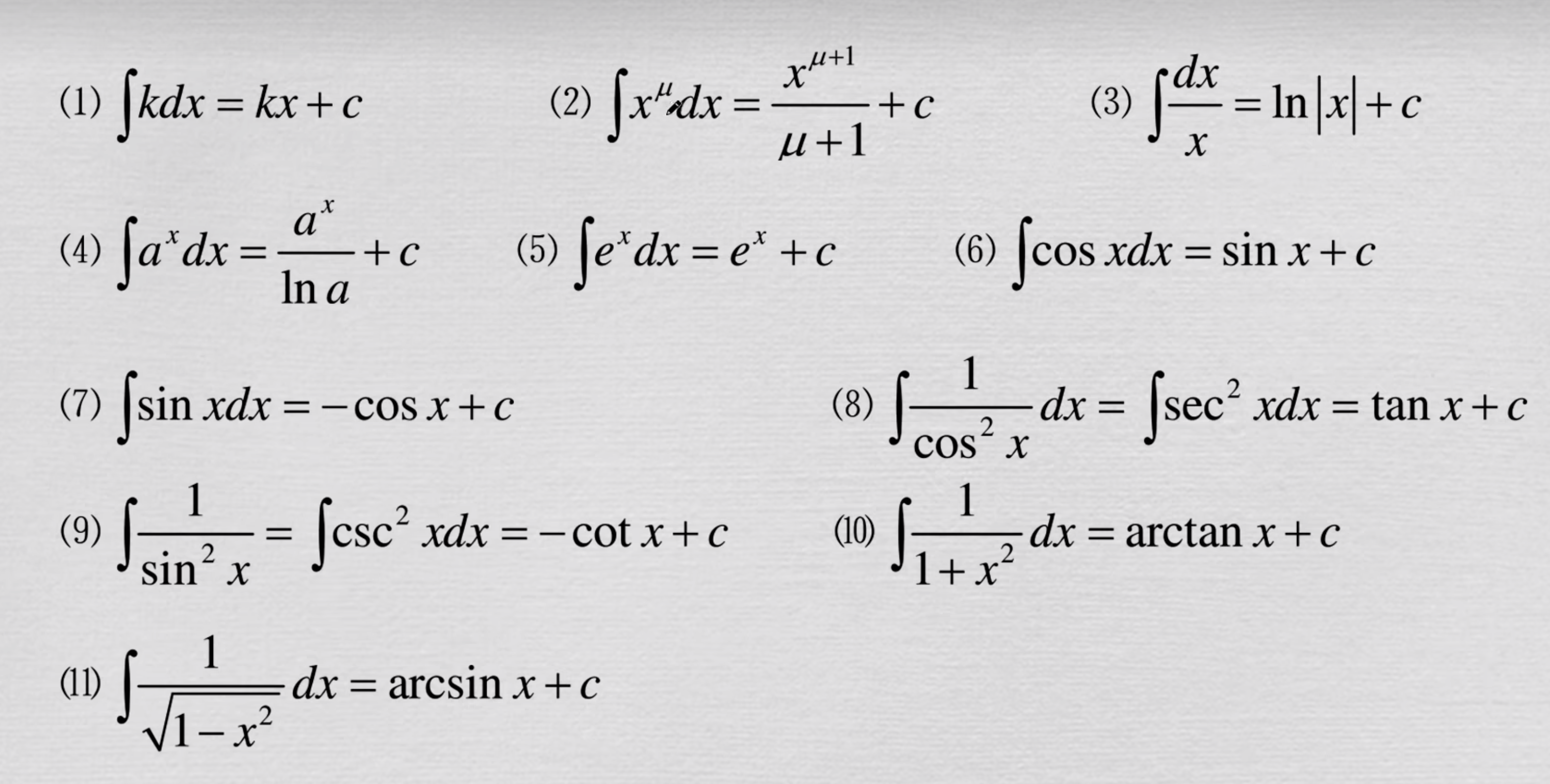微积分
参考视频
参考视频
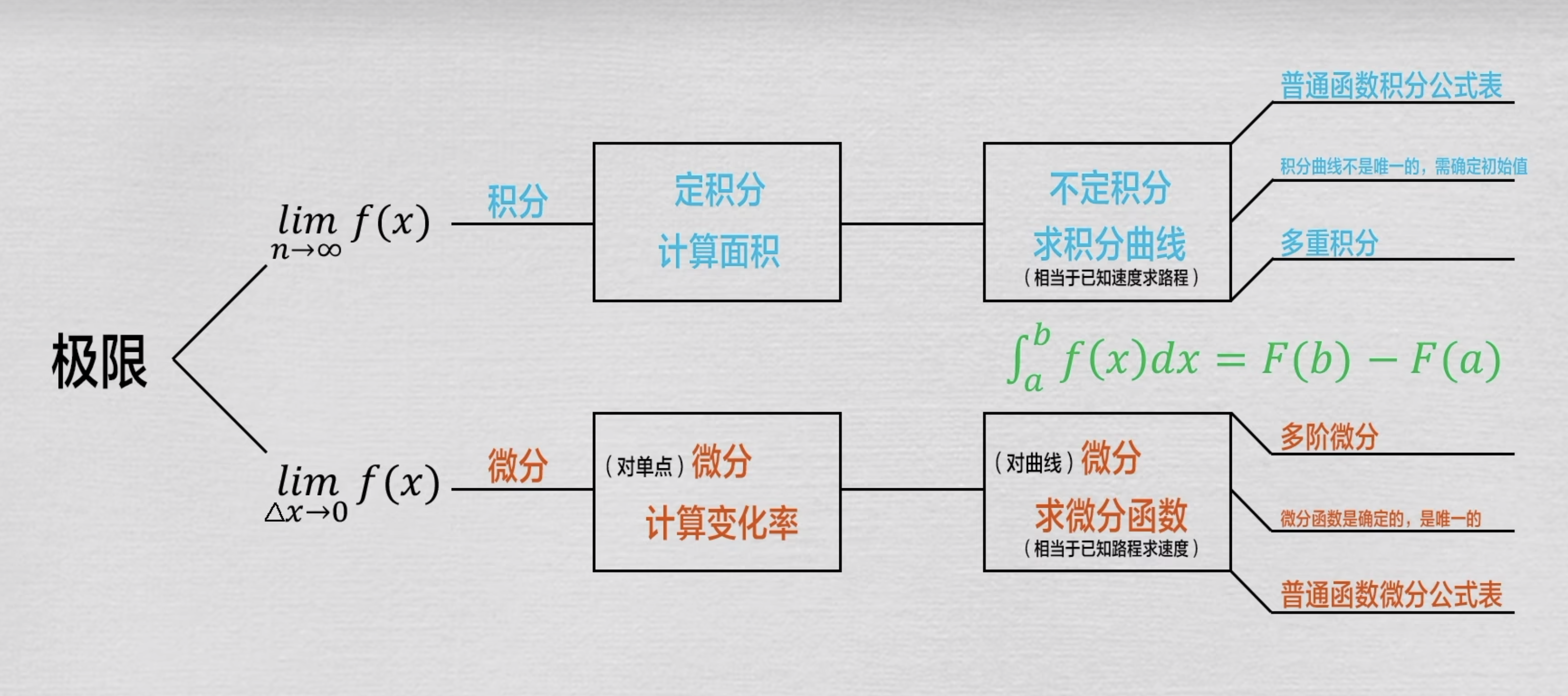
微积分:把无穷引入计算后,产生的一套计算方法
- 趋向于无穷小的计算叫微分(differential)
- 趋向于无穷大的计算叫积分(integral)
微积分能解决什么问题
- 计算曲边图形的面积
- 计算曲线上某个点的(切线、切线的斜率、变化率、导数、速度、微分)
- 切线、切线的斜率、变化率、导数、速度、微分其实说的都是一回事(时间路程函数上某个时间点的实时速度)
- 切线:经过曲线上某个点,有且仅有一条与之相交的直线
求曲面梯形的面积

求曲面梯形的近似值(直接求梯形面积)
2(1+4)∗1=2.5
沿梯形的高的中心做一条垂线,这样求得的近似值误差更小
2(1+(3/2)2)∗(1/2)+2((3/2)2+4)∗(1/2)=2.375
依次类推,我们可以把梯形分成N份,N越大,近似值误差越小
最终求得如图所示的通式
37+6n21
但是,无论N多大,我们都无法求得真实面积,只能求得跟真实面积误差极小的面积
当N不断增大的过程中,37+6n21永远不能等于,但可以无限接近的那个值 = 37
可以用极限表示,如下:
n→∞lim(37+6n21)=37
如果一个混合运算中含有极限技巧,那么它就属于微积分范畴
在微积分里面求一块图形的固定面积,叫作定积分
∫12x2dx
求切线的斜率
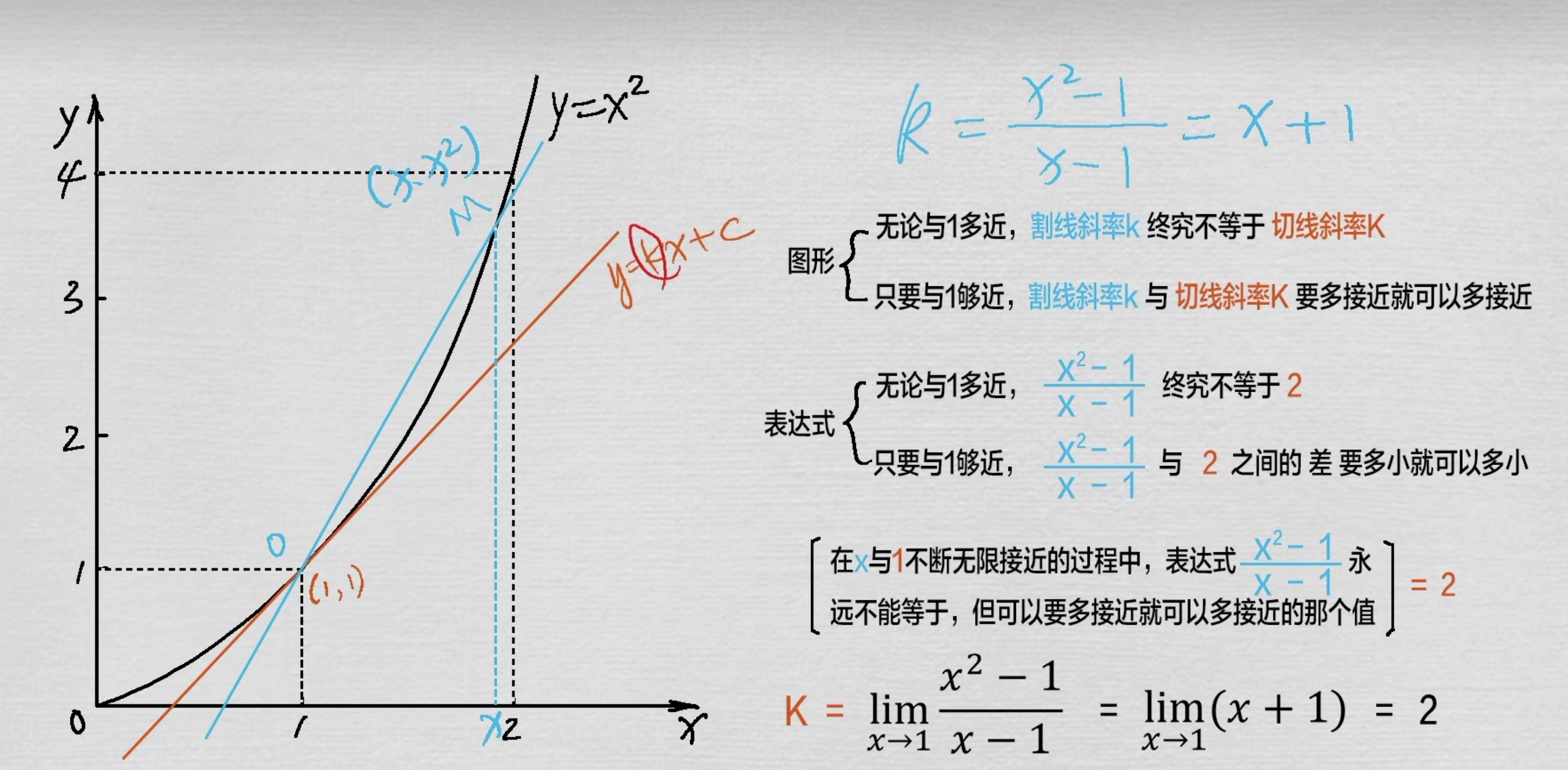
割线OM的斜率,k=x−1x2−1=x+1
切线的斜率,k=x→1limx−1x2−1=x+1=2
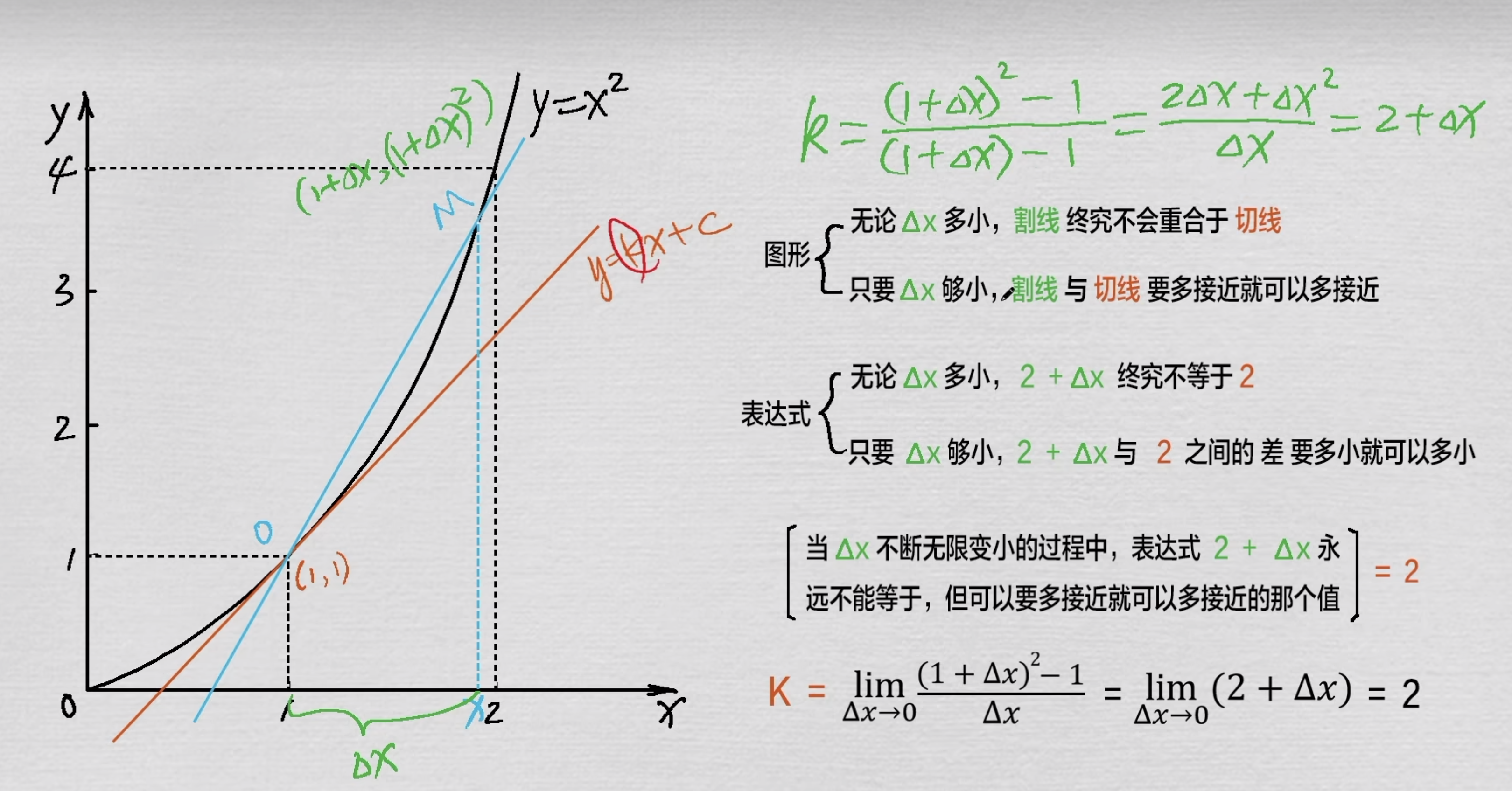
引入△后,k=△x→0lim(1+△x)−1(1+△x)2−1=2+△x=2
我们习惯把使用△x趋向于0这种计算方式叫微分
△x写作dx,△f(x)写作df(x)
dxdf(x)叫作导数,也可以写作f′
对一条函数曲线使用微分可以得到一条新的曲线(相当于把路程函数的速度函数给求出来了)
k=△x→0lim(x+△x)−x(x+△x)2−x2=2x+△x=2x
如果对一条函数曲线微分,得到的就是微分函数,也就是说,速度函数是路程函数的微分函数
实际应用中,求单个点的速度,一般会先求速度函数,再由速度函数求得单个点的实时速度(或者说变化率)
- 对路程函数进行微分可以得到速度函数(速度函数是路程函数的一阶微分函数)
- d(x2)=2xdx
- dxd(x2)=2x
- 对速度函数进行微分可以得到速度函数的变化率函数(加速度函数是路程函数的二阶微分函数)
- d(2x)=2dx
- dxd(2x)=2
- 对速度函数的变化率函数进行微分可以得到速度函数的变化率函数的变化率函数(加速度函数的变化率函数是路程函数的三阶微分函数)
- d(2)=0dx
- dxd(2)=0
- 还可以一直微分下去...
- d(0)=0dx
- dxd(0)=0
路程函数与速度函数相互转换


匀速直线运动的路程函数y=2t,那么它的速度函数用肉眼就能看出来就是2
反过来,如果速度函数是y=2,那么路程函数就是y=2t+c(因为起点不同,所以需要一个常量c)
均加速直线运动的速度函数是y=2t,那么它的路程函数就是y=t2+c(通过三角形面积)
反过来,如果路程函数是y=t2+c,用肉眼就无法看出它的速度函数了,可以使用微积分计算(求切线)
再升级一下,如果速度函数y=t2,用肉眼也无法看出它的路程函数了,可以使用微积分计算(求面积)
再升级一下,如果速度函数是一个毫无规则波浪线,那么就无法通过微积分来计算它的路程函数了(不收敛)
但是速度函数和路程函数之间的这些关系依然存在,这时候如果要解决速度函数与路程函数之间的变化关系,就得发明新的算法
普通函数微分公式表
相当于把普通函数当成路程函数,把它们的速度函数计算出来
当我们看到微分公式表的时候,应该意识到它们的内核都是极限,它们都是由△x趋向于无穷小这种方法算出来的
趋向于0或者趋向于一个比x小的固定值,都可以统称为趋向于无穷小
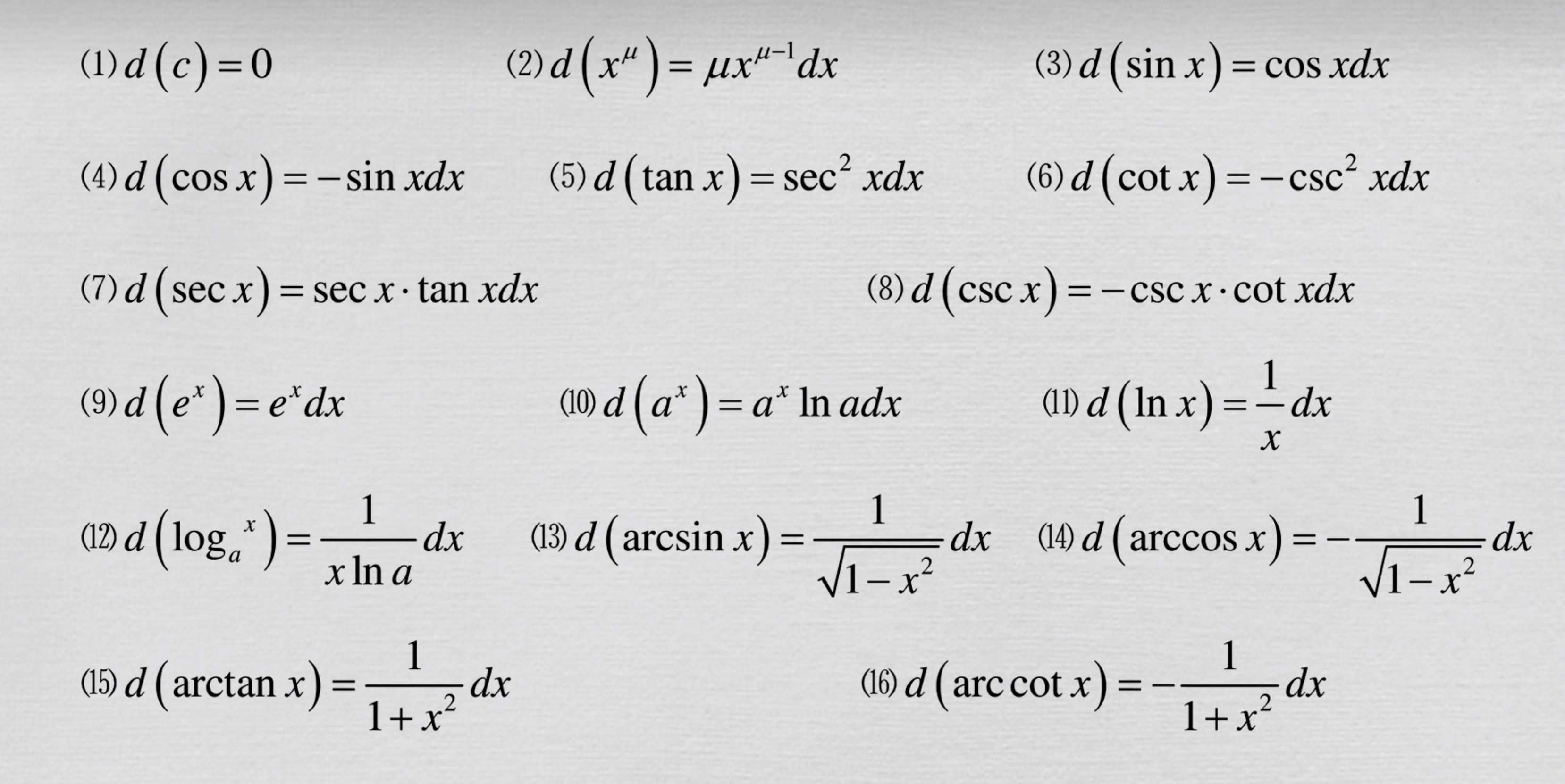
普通函数的积分公式表
我们可以通过算面积把速度函数的路程函数的通式给算出来
它们可以描述为速度函数的原函数或积分曲线或积分函数
我们把由速度函数计算路程函数的过程叫不定积分
换句话说对速度函数的不定积分得到的就是路程函数的通式
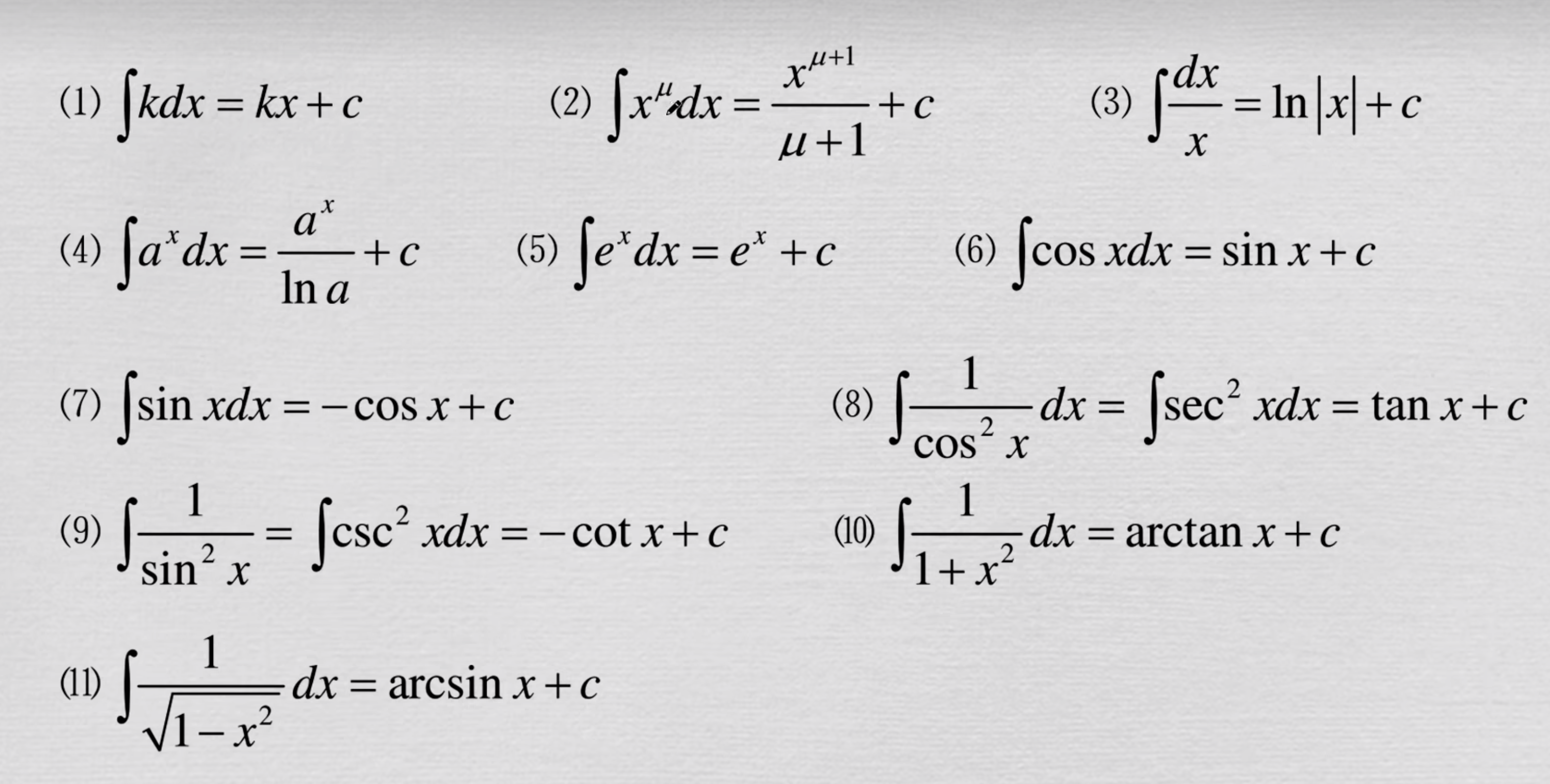
导数
原函数乘以常数:dxd[cf(x)]=cf′(x)
两个函数相加:dxd[f(x)+g(x)]=f′(x)+g′(x)
两个函数相乘:dxd[f(x)g(x)]=f′g+fg′
极限
极限不存在的判定
极限的判断有一个最直接的作用就是判断这个函数是不是连续的
如何判断一个函数是不是连续,可以简单归纳为一句话
函数在某一点上的函数值等于在这个点上的极限(有函数值、有极限值、并且相等)
f′(x)=△x→0lim△xf(x+△x)−f(x)
设 limf(x)=A,limg(x)=B,则:
- lim(f(x)±g(x))=A±B
- lim(f(x)g(x))=AB
- lim(cf(x))=cA
- limg(x)f(x)=BA B ≠ 0
- limf(x)1=A1 A ≠ 0
- lim[f(x)]n=AnA∈Z+
总结
微分:对原函数进行求导
- f′(t)=dtdf(t)
- (f(t)+c)′=f′(t)
积分:在已知导数时,试图找出原函数的行为
不定积分:找出原函数的表达式
- ∫f′(t)dt=f(t)+c
- 不唯一
- 常数C
∫cf(x)dx=c∫f(x)dx
∫(f(x)+g(x))dx=∫f(x)dx+g(x)dx
定积分:求出一个数值
- ∫abf′(x)dx=f(b)−f(a)
- [f(x2)+c]−[f(x1)+c]=f(x2)−f(x1)
复合函数
dxd[f[g(x)]]=dgdfdxdg
扩展
f−1(x) 是 f(x) 的反函数,相当于 x(f),不是f的负一次方
反函数存在的条件是:该函数中x与y之间的对应是一对一
设y=f(x)是一个可导函数,有唯一的反函数 x=f−1(y)
将y=f(x)代入x=f−1(y),就得到x=f−1(f(x))
根据复合函数求导法则(g、f都表示函数,顺序可调整)
dxdg(f(x))=df(x)dg(f(x))dxdf(x)=g′(f(x))f′(x)
将f−1(x)看作是上式中的g(x),就有
1=dxdx=dxdf−1(f(x))=(f−1)′(f(x))f′(x)
所以有
(f−1)′(f(x))=f′(x)1
即有
(f−1)′(y)=f′(x)1=f′(f−1(y))1