线性代数

参考视频

行列式

二阶行列式：两行两列4个元素，主对角线的元素相乘 - 次对角线的元素相乘 = 某个数

主对角线："\" 次对角线："/" 行列式符号："|...|"

行列式的某个元素可以用：$a_{ij}$表示，i为行标、j为列标

$D = | a_{ij} |$

一阶行列式等于它自身：$| a_{11} | = a_{11}$

三阶行列式

$\begin{vmatrix} {a_{11}}&{a_{12}}&{a_{13}}\\ {a_{21}}&{a_{22}}&{a_{23}}\\ {a_{31}}&{a_{32}}&{a_{33}} \end{vmatrix}$

也可以用二阶行列式那样划线的方法计算

$a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{13} a_{22} a_{31} - a_{12} a_{21} a_{33} - a_{11} a_{23} a_{32}$

n级标准排列

n级标准排列（自然排列）：由1,2,3,...,n组成的一个有序数组（中间不能缺数）

逆序：大数排在小数的前面

逆序数：逆序的总数

4213的逆序数为：4（4>2>1>3，2>1），表示为：N(4213)=4

N(123...n)=0

N(n,n-1,...,3,2,1) = (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2

偶排列：逆序数为偶数的排列

奇排列：逆序数为奇数的排列

对换：交换两个数

一个排列经过一次对换奇偶性会改变

n级排列中奇排列和偶排列的个数相等，各占一半（n! / 2）

n阶行列式

n阶行列式展开的第一种定义：按行展开

这里以3阶为例：

$a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{13} a_{22} a_{31} - a_{12} a_{21} a_{33} - a_{11} a_{23} a_{32}$

行标取标准排列：123

列标取所有的可能：一共6种

• 123，N(123)=0，偶排列
• 231，N(231)=2，偶排列
• 312，N(312)=2，偶排列
• 321，N(321)=3，奇排列
• 213，N(213)=1，奇排列
• 132，N(132)=1，奇排列

$\begin{vmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{n1}}&{a_{n2}}&{\cdots}&{a_{nn}} \end{vmatrix} = \displaystyle\sum_{j_1j_2...j_n}(-1)^{N(j_1j_2...j_n)}a_{1j_1}a_{2j_2},...,a_{nj_n}$

n阶行列式展开的第二种定义：按列展开

行标取所有的可能

列标取标准排列

$\displaystyle\sum_{i_1i_2...i_n}(-1)^{N(i_1i_2...i_n)}a_{i_11}a_{i_22},...,a_{i_nn}$

$\displaystyle\sum(-1)^{N(i_1i_2...i_n)+N(j_1j_2...j_n)}a_{i_1j_1}a_{i_2j_2},...,a_{i_nj_n}$

三角行列式

下三角行列式：主对角线上方全为0，结果等于主对角线元素相乘（符号为正，标准排列）

对角型行列式：主对角线上、下方全为0，结果等于主对角线元素相乘（符号为正，标准排列）

次下三角行列式：次对角线上方全为0，结果等于次对角线元素相乘（符号为$-1^{\frac{n(n-1)}{2}}$，降序排列）

次上三角行列式：次对角线下方全为0，结果等于次对角线元素相乘（符号为$-1^{\frac{n(n-1)}{2}}$，降序排列）

次对角型行列式：次对角线上、下方全为0，结果等于次对角线元素相乘（符号为$-1^{\frac{n(n-1)}{2}}$，降序排列）

转置

$D = \begin{vmatrix} 1&2&3\\ 1&1&1\\ 8&8&8 \end{vmatrix}$

$D^T = \begin{vmatrix} 1&1&8\\ 2&1&8\\ 3&1&8 \end{vmatrix}$

转置也可以用D'表示，但是容易跟导数搞混，所以一般用$D^T$的较多

两次转置等于本身

行列式的性质

1、行列式转置后，其值不变

2、两行互换，值变号

3、两行或两列对应相等，行列式的值等于0

4、某一行都乘以k，等于用k乘以D。即：行列式某一行都有公因子k，k可以提到外面去。行列式所有元素都有公因子k，k朝外提$k^n$

5、两行或两列对应成比例，行列式的值等于0（3、4合并可得5）

5'、某一行全为0，行列式等于0（0提出来乘以行列式必定等于0）

PS：3、5、5'，都能推出行列式等于0，但行列式等于0不一定就是3、5、5'其中之一

6、行列式的某一行是两项和，该行列式可以拆分为两个行列式相加（是和的那一行分开，其余行保持不变）

$\begin{vmatrix} 1&2&3\\ 7+8&2+3&9+10\\ 8&8&9 \end{vmatrix} = \begin{vmatrix} 1&2&3\\ 7&2&9\\ 8&8&9 \end{vmatrix} + \begin{vmatrix} 1&2&3\\ 8&3&10\\ 8&8&9 \end{vmatrix}$

通常我们习惯使用性质7来凑上三角行列式，来求行列式的值

解题技巧，利用性质2把易于消其他行的行换到第一行去

解题规范，先处理第一列、再第二列、再第三列，以此类推

第一列处理完后，第一行不再参与，第二列处理完后，第二行不再参与，以此类推

行列式展开

余子式：把行列式指定元素的所在行和所在列划掉，剩下的子式就是余子式，符号：$M_{ij}$

代数余子式：$(-1)^{i+j}$ 乘以余子式，符号：$A_{ij}$

定理（按某行或某列展开）

$D=a_{i1}A_{i1}+a_{i2}A_{i2}+...+a_{in}A_{in}$

$D=a_{1j}A_{1j}+a_{2j}A_{2j}+...+a_{nj}A_{nj}$

$\begin{vmatrix} 1&1&2\\ 0&1&0\\ 2&3&5 \end{vmatrix} = 1 \times (-1)^{1+1} \begin{vmatrix} 1&0\\ 3&5 \end{vmatrix} + 1 \times (-1)^{1+2} \begin{vmatrix} 0&0\\ 2&5 \end{vmatrix} + 1 \times (-1)^{1+3} \begin{vmatrix} 0&1\\ 2&3 \end{vmatrix}$

拉普拉斯定理

比如：以下式子第一二行和第一二列划掉

$\begin{vmatrix} 1&2&3&4\\ 1&1&2&5\\ 1&1&0&8\\ 9&9&9&10 \end{vmatrix}$

那么，$\begin{vmatrix} 1&2\\ 1&1 \end{vmatrix}$就是2阶子式，$\begin{vmatrix} 0&8\\ 9&10 \end{vmatrix}$就是余子式

代数余子式：$(-1)^{1+2+1+2}$ 乘以余子式（1+2+1+2：把划掉的行列全部相加）

行列式相乘

行乘列（行列元素依次对应相乘），再累加

$\begin{vmatrix} 1&1&1\\ 2&0&0\\ 0&0&3 \end{vmatrix} \times \begin{vmatrix} 1&2&3\\ 1&3&2\\ 3&2&1 \end{vmatrix} = \begin{vmatrix} 5&7&6\\ 2&4&6\\ 9&6&3 \end{vmatrix}$

加边法

$\begin{vmatrix} 1+a_1&1&{\cdots}&1\\ 1&1+a_2&{\cdots}&1\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ 1&1&1&1+a_n \end{vmatrix}$

$\begin{vmatrix} 1&1&1&1&1\\ 0&1+a_1&1&{\cdots}&1\\ 0&1&1+a_2&{\cdots}&1\\ {\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}\\ 0&1&1&1&1+a_n \end{vmatrix}$

这样加的话，按照第一列展开，还是等于原来的值 $(-1)^{1+1}$ 乘以1再乘以原行列式（其余项都为0，所以乘积也为0）

三叉型行列式

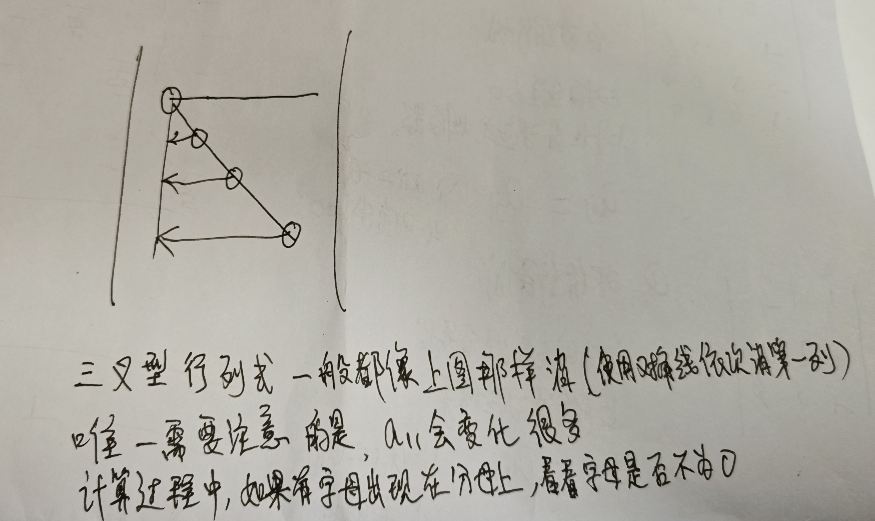
范德蒙德行列式

$\begin{vmatrix} 1&1&{\cdots}&1\\ x_1&x_2&{\cdots}&x_n\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ x_1^{n-2}&x_2^{n-2}&{\cdots}&x_n^{n-2}\\ x_1^{n-1}&x_2^{n-1}&{\cdots}&x_n^{n-1} \end{vmatrix}$

∏($x_i-x_j$) （1 <= j < i <= n） （∏为连乘符号，连乘1次方的那行，第1行可以认为是0次方）

注意：i大于j，不是大于等于j，如果相等，那么$x_i-x_j$必定有一个等于0，那么连乘后也为0

$\begin{vmatrix} 1&1&1\\ 2&3&4\\ 4&9&16 \end{vmatrix}$

• 当j=1时，x=2,3，$(x_2-x_1) \times (x_3-x_1) = (3 \times 2)(4 \times 2)$
• 当j=2时，x=3，$(x_3-x_2) = (4 \times 3)$

反对称行列式

$\begin{vmatrix} 0&1&2&3\\ -1&0&-5&6\\ -2&5&0&8\\ -3&-6&-8&0 \end{vmatrix}$

因为$a_{ii} = -a_{ii}$，所以对角线=0

奇数阶的反对称行列式=0

证明：每行提出一个-1，会推导出 $D=-D^T$，而 $D=D^T$，所以D=0

对称行列式

因为$a_{ii} = a_{ii}$，所以对角线没有要求

克莱姆法则

• 含有N个方程N个未知量，即：方程的个数要等于未知数的数量
• D!=0，则$x_j=\frac{D_j}{D}$（D是方程组的系数行列式，$D_j$是把D的j列换成常数项后的行列式）

$\begin{cases} x_1 + x_2 + x_3=1\\ x_1 - x_2 + 5x_3=6\\ -x_1 + x_2 + 6x_3=9 \end{cases}$

$D=\begin{vmatrix} 1&1&1\\ 1&-1&5\\ -1&1&6 \end{vmatrix} D_1=\begin{vmatrix} 1&1&1\\ 6&-1&5\\ 9&1&6 \end{vmatrix} D_2=\begin{vmatrix} 1&1&1\\ 1&6&5\\ -1&9&6 \end{vmatrix} D_3=\begin{vmatrix} 1&1&1\\ 1&-1&6\\ -1&1&9 \end{vmatrix}$

$x_1 = \frac{D_1}{D} \quad x_2 = \frac{D_2}{D} \quad x_3 = \frac{D_3}{D}$

计算量非常大，一般不常用

齐次方程组

$\begin{cases} x_1 + x_2 + x_3=0\\ x_1 - x_2 + 5x_3=0\\ -x_1 + x_2 + 6x_3=0 \end{cases}$

齐次方程组至少有0解，即：$x_1 x_2 x_3$ 全为0

齐次方程组（方程个数=未知数个数），有非0解 <=> D=0